Meccanica di un punto materiale soggetto ad una forza costante.
| N |
V |
LB |
Titolo della lezione. |
2IA |
2IB |
2M |
| |
|
|
Adolescenza. Circolo vizioso,
circolo virtuoso. |
|
|
|
| |
|
|
Settembre
|
|
|
|
| |
|
|
01 Moto sul piano inclinato. |
|
|
|
| |
|
|
02 Moto sul piano inclinato. Durata
discesa. VrfCrz (verifica e correzione) |
|
|
|
| |
|
|
03 Moto sul piano inclinato. Durata
discesa.. Analisi dati di classe. |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
Arg ini anno:
- Meccanica di un corpo puntiforme soggetto a forza k.
- MAK moto ad accelerazione costante.
|
12 |
|
|
| |
|
|
Si riparte da:
Gittata in funzione della velocita' di decollo. |
12 |
|
|
| |
|
|
Forza gravita' punta centro Terra, ma esso non attira ! |
12 |
|
|
| |
|
|
-
Velocitą di caduta verticale di una pallina sganciata.
- Rallentare
il moto di caduta, con un piano inclinato, per poterlo studiare.
- MAK: esempio
spiegazione di Galileo.
- Tb oraria.
-
La legge di Galileo per il moto dei gravi.
-
MAK (1/2)t
(1/4)s.
|
|
|
|
| |
|
|
MAK. Moto =
tempo trascorso + spazio percorso. |
|
|
|
| |
|
|
MAK. 256mm ½t¼s
2t4s. Lo stesso MAK, con tempi e spazi misurati con unita' diverse dal
totale. |
|
|
|
| |
|
c |
Tb oraria 30 passi, e dis livelli. |
|
|
|
| |
|
c |
Destra 1
passo, giu' 1 livello. |
|
|
|
| |
|
c |
Tanti
passi quanto lunghi. |
|
|
|
| |
|
|
Errore di start e stop
watch. |
|
|
|
| |
|
|
|
|
|
|
| |
|
c |
Fisica 1: Libro
Ruffo. La nostra sintesi estrema. |
26 |
|
|
| |
|
|
La conoscenza e
la metafora del territorio. |
26 |
|
|
| |
|
|
|
|
|
|
| |
|
|
Ottobre
|
|
|
|
| |
|
|
Caduta verticale di un grave. (1/2)t (1/4)s. |
1 |
1 |
1 |
| |
|
|
Caduta verticale di un grave. (1/2)t (1/4)s. Crz. |
3 |
3 |
3 |
| |
|
|
Caduta verticale di un grave. (1/2)t (1/4)s. 2D montaggio alv. 2C
ms alv |
|
11 |
11 |
| |
|
|
E' un MAK ? |
|
26 |
|
| |
|
|
|
|
|
|
| |
|
|
Novembre
|
|
|
|
| |
|
Lab |
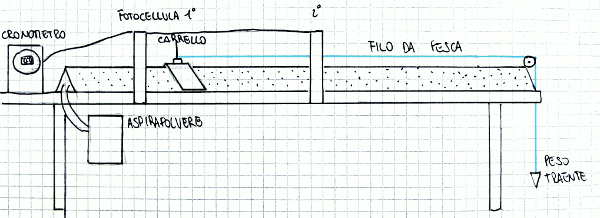
Slitta tirata da un peso in caduta.
|
5 |
8 |
8 |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
ANNI PRECEDENTI
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
Campionare una grandezza
variabile continua. |
|
|
|
| |
|
|
Discesa rettilinea di sfera su piano inclinato (rotolare senza
strisciare), legge oraria. |
|
|
|
| |
|
|
Discesa volano su piano inclinato (rotolare senza strisciare), legge
oraria. |
|
|
|
| |
|
|
Moto di una sfera sul piano inclinato. |
|
|
|
| |
|
|
Moto sotto l'effetto del peso. Mappa argomenti.
|
|
|
|
| |
|
|
Grave. Moto di un grave.
|
|
|
|
| |
|
|
- ix Moto di un grave, libero, peso costante.
-
ix Lancio
orizzontale.
-
Incrementi di posizione.
- Parabola forma standard:
.odg|pdf. App studio:.odg|pdf
-
Raffinare campionamento.
|.odg|pdf
-
Disegni. FC
.xls |
ods|pdf Man.odg |pdf
- ix Lancio
qualsiasi, moto parabolico.
-
Disegni.
- ix Caduta verticale.
ix Moto a=k ad accelerazione
costante.
-
Dis
- mak_tb.ods
tb ricopiata nel cc_mak.odg
in s = t² vm = t
|
|
|
|
| |
|
|
-
Velocitą di caduta verticale di una pallina
sganciata.
- MAK
(1/2)t (1/4)s. |
MAK. Simbolo
grafico
- MAK vs MVK.
- E oltre
la fine del moto? Come proseguirebbe se non finisse?
|
|
|
|
| |
|
|
- Moto =
tempo trascorso + spazio percorso.
- MAK. 256mm
½t¼s 2t4s.
|
|
|
|
| |
|
|
La velocita' finale dipende solo dal dislivello e non dalla
traiettoria (partendo sempre da fermo, o partendo sempre con la stessa velocita').
L'incremento di v dipende solo dal dislivello e non dalla
traiettoria. ∆v dipende solo da ∆H e non dalla traiettoria |
|
|
|
| |
|
|
Caduta verticale di un grave. (1/2)t (1/4)s. |
|
|
|
| |
|
|
MAK. Grafico lineare a pezzi s=f(t) t = 1 2 4. |
|
|
|
| |
|
|
MAK. 256mm
½t¼s 2t4s. |
|
|
|
| |
|
|
Caduta verticale di un grave. Errori di misura di tempo e spazio. |
|
|
|
| |
|
|
s = t² vm
= t |
s = ½at² vm = ½at |
|
|
|
| |
|
|
y = x2
numerico e grafico extra 2C |
|
|
|
| |
|
|
Rel1.
Caduta verticale di un grave. (1/2)t (1/4)s. |
|
|
|
| |
|
|
Spiegata e vista su vp 2a faccia
rel1. |
|
|
|
| |
|
|
Ottobre
|
2B |
2C |
2D |
| |
|
|
Caduta verticale di un grave quasi. |
|
|
|
| |
|
|
MAK vs MVK.
|
|
|
|
| |
|
|
E oltre la fine del moto? Come proseguirebbe se
non finisse? |
|
|
|
| |
|
|
Come "Programmare
animazione SVG", iniziativa fallita. |
|
|
|
| |
|
|
Nel tubo a vuoto:
il piombino e la piuma, cadono di ugual moto. |
|
|
|
| |
|
|
Scivolo a cuscino d'aria. |
|
|
|
| |
v |
|
MAK su scivolo a cuscino d'aria inclinato ½t¼s 2t4s. |
|
|
|
| |
|
|
Slitta tirata da un peso in caduta, ridotto a:
La slitta sullo scivolo a cuscino d'aria, e i 3 principi. |
|
|
|
| |
|
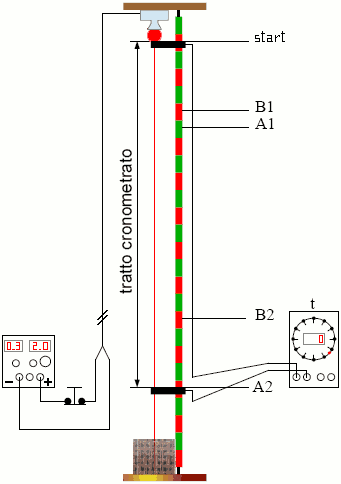
|
Come
misurare la lunghezza del tratto cronometrato dalla coppia di
fotocellule, sullo scivolo a cuscino d'aria ? |
|
|
|
| |
|
|
Slitta tirata da un peso in caduta, visto Foglio calc
.ods|pdf |
|
|
|
| |
|
|
Slitta tirata da un peso in caduta.|
MAK. s1 s2
∆t determinano l'accelerazione. |
|
|
|
| |
|
|
MAK. s1 s2
∆t determinano l'accelerazione. |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
Novembre
|
2B |
2C |
2D |
| |
|
|
Oscillazioni molla-peso. |
|
|
|
| |
|
|
Velocita' di discesa in funzione del dislivello. |
|
|
|
| |
|
|
la=f(ld) lunghezza_di_arresto inFUNZIONEdi
lunghezza_di_discesa |
|
|
|
| |
|
|
Cose e azioni. | Non tutte le azioni
sono moti. |
Schema. |
Mapparg. | Unita' di
misura, e grandezza. |
|
|
|
| |
|
|
Problema della brachistocrona. |
Pista piu' semplice: piano inclinato e tratto orizzontale. |
|
|
|
2B gio 25ott elezione rappresentanti.
4 ottobre 2012 Giovedi. Patrono di Massa, S.Francesco