^^Velocita' discesa in funzione del dislivello. 2012.
Qui relazione,
la'
approfond.
Caso complementare:
= dislivello, ≠ inclinazioni
Indicazioni per redigere la relazione. (Le indicazioni non ricopiare).
- Non ricopiare gli approfondimenti.
- L'esp e' fatto da 2 esp: 1:
Velocita' discesa causata da: = dislivello, ≠ inclinazioni.;
2: quello qui descritto.
- Disegno del solo esp2 in scala 1:10 per: le altezze discese; lunghezze gittata;
altezza decollo; usando i valori ideali di gittata (calcolati qui avanti). Traiettoria e inclinazione, sensate. E' il dis
da fare
a inizio relaz.
- Ricopiare cio' che segue.
Descrizione semplice del fenomeno
Una sfera rotola su una retta inclinata, che termina con un raccordo
orizzontale, che la lancia in aria, vola, e cade sul pavimento.
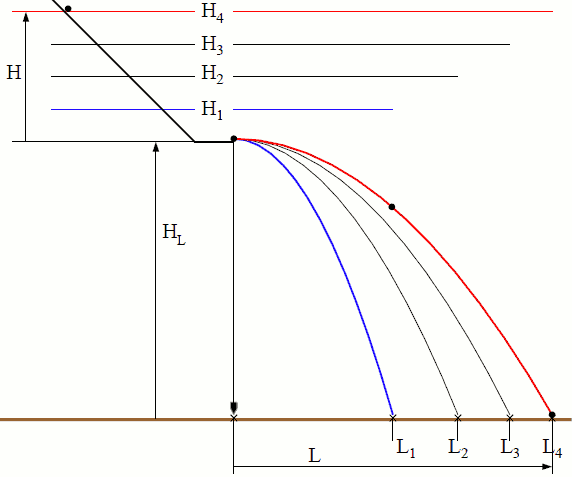
Il fatto fondamentale che ci interessa notare e':
- per moltiplicare per 2 la gittata
(nel disegno da L1 a L4)
- occorre moltiplicare l'altezza per 4 (nel
disegno da H1 a H4).
EC energia cinetica. EG
en gravitazionale.
L'EC alla fine della discesa e' = all'EG
all'inizio. In accordo col principio di conservazione dell'energia.
Scopo. che velocita' sara' prodotta dalla trasformazione di energia ?
Per misurare la velocita'.
v
velocita di decollo di un lancio orizzontale e' direttamente proporzionale alla
gittata
Per misurare EG
EG = P*H.
Teoria. L = k√H
Per l'elaborazione dei risultati dell'esp consideriamo una formula
semplificata che evidenzia solo l'aspetto che ci interessa.
dim:
- L = kv dove k e' il tempo di volo. E v dipende da
Ec ...
- v = √(2Ec /M) . E EC dipende da EG
...
- EC = EG . E EG dipende da H ...
- EG = P*H.
- Sostituendo si ottiene l'asserto.
Apparato sperimentale
- Piano orizzontale di lancio. 85cm = HL altezza del piano orizzontale di lancio;
altezza rispetto al piano di
impatto. Cioe' il dislivello del volo, dal decollo all'impatto.
- Guida per la discesa. Per fissarla: nastro adesivo per qualche centimetro sul fondo interno della
guida, e continua aderendo al bordo del tavolo.
- Sfera.
Accorgimenti sperimentali
-
Attenzione, non confondere
>>>
- La sfera deve rotolare senza strisciare. Se scivola l'effetto sulla velocita'
cambia.
Gittata ideale
| |
cm |
cm |
cm |
cm |
cm |
| N |
H |
L |
∆H |
∆L |
L/√H |
| 0 |
0 |
0 |
+10 |
+49 |
|
| 1 |
10 |
49 |
+10 |
+20 |
15,5 |
| 2 |
20 |
69 |
+10 |
+16 |
15,5 |
| 3 |
30 |
85 |
+10 |
+13 |
15,5 |
| 4 |
40 |
98 |
/// |
/// |
15,5 |
|
|
Nelle condizioni:
- HL= 85cm
- lancio orizzontale
- sfera omogenea che
rotola senza strisciare
- tutta l'energia gravitazionale si trasforma
in en cinetica, cioe' zero dissipazione di energia
- resistenza aria
trascurabile.
|
Studiare come la gittata dipende dall'altezza della discesa di lancio
Procedimento
- 3 lanci per ogni fissate altezza
- 4 diverse altezze
Dati di Ratti Samuele 2B 2013-14
.ods
| |
|
|
|
|
|
|
| N |
H |
L |
|
√H |
|
L/√H |
| 0 |
0 |
0 |
|
0 |
|
|
| 1 |
10 |
28,4 |
|
3,16 |
|
12,0 |
| 2 |
20 |
43,7 |
|
4,47 |
|
12,9 |
| 3 |
30 |
58,8 |
|
5,47 |
|
12,3 |
| 4 |
40 |
75,4 |
|
6,32 |
|
13,2 |
|
|
L/√H idealmente dovrebbe essere costante, invece ha una variazione
percentuale 9,5%.
Coi nostri mezzi possiamo ritenerlo un risultato discreto.
Chi ha dati migliori li usi.
|
Fare il grafico cartesiano della funzione LfH, con le dimensioni qui
indicate.
| Asse |
Lung cm |
Scala 1cm: |
| x = H |
10 |
5 |
| y = L |
10 |
10 |
Graficare nello stesso rettangolo cartesiano sia i dati ideali che quelli sperimentali.
Vedi .ods
Conclusioni
- La velocita' alla fine della discesa non e' dir prop all'altezza della
discesa.
In termini energetici: la velocita' non e' dir prop all'en cinetica.
- I dati disponibili non permettono di confermare la forma della
dipendenza prevista, e cioe' L/√H = kostante, con una approssimazione
< 10%.
Approfond
|
1 |
|
| Ec =
|
|
Mv2 v = √(2Ec /M) |
|
2 |
|
|
|
| Ec |
Energia cinetica del pm (punto materiale) |
| M, v |
massa e velocita' del pm |
|
Teoria. Si puo' calcolare-prevedere la velocita' alla fine della discesa, e
la lunghezza del lancio.
Per l'elaborazione dei risultati dell'esp consideriamo una formula
semplificata che evidenzia solo l'aspetto che ci interessa:
v = k√H la velocita' e' dir prop alla radice quadrata
dell'altezza della discesa.
L = kv = k√H la lunghezza del lancio e' dir prop √H
Cerchiamo di capire in un caso particolare la validita' della formula.
- La velocita' a fine discesa e' indipendente dalla traiettoria, per
considerazioni energetiche e esp1. Quindi per calcolarla considero il caso
comodo della discesa verticale.
- Il moto di discesa e' un MAKv00, un moto ad acceleraz costante, con
v0=0 partenza a velocita' 0.
- Per raddoppiare la velocita', occorre un tempo doppio, poiche' nel
MAKv00 v=at la velocita' e' dir prop al tempo (trascorso dalla partenza a
velocita' 0).
- Ma se il tempo raddoppia (t*2), lo spazio quadruplica (s*4). In simboli
2t4s.
- Allora per raddoppiare la velocita' occorre uno spazio quadruplo. In
simboli 2t4s2v.
- Confrontiamo con la predizione formula. Premesso: v1 = k√H1 v4
= k√H4 H4 = 4H1
Segue v4 = k√H4 = k√(4H1)
= k√4√H1 = k2√H1 = 2k√H1
= 2v1
Dati di altri sperimentatori
Dati di Bertellotti 2B 8-11-2012.ods
| |
|
|
|
|
|
|
|
|
| N |
H |
L1 |
L2 |
L3 |
|
L |
∆L |
L/√H |
| 0 |
0 |
0 |
0 |
0 |
|
0 |
+28,4 |
|
| 1 |
10 |
28 |
28,2 |
29 |
|
28,4 |
+15,3 |
9,0 |
| 2 |
20 |
43,7 |
44,5 |
42,8 |
|
43,7 |
+15,1 |
9,8 |
| 3 |
30 |
59,5 |
59 |
58 |
|
58,8 |
+16,6 |
10,7 |
| 4 |
40 |
74 |
74,3 |
78 |
|
75,4 |
/// |
11,9 |
|
|
L valor medio di L1 L2 L3
L/√H idealmente dovrebbe essere costante, invece ha una variazione
percentuale 28,5%. Si poteva fare di meglio.
Chi ha dati migliori li usi.
|
Conclusioni
I dati disponibili non permettono di confermare la forma della
dipendenza prevista, e cioe' L/√H = kostante, poiche' cio' che
dovrebbe essere una costante, ha invece una variabilita' del 28%, ed e'
troppo.
Talk
Scopo. Studiare la relazione tra: l'en cinetica di un corpo, e la sua velocita'.
Il teatro operativo proposto soddisfa questo scopo, poiche':
- l'altezza della discesa misura l'en cinetica del corpo alla fine della
discesa. EC = kH
- la lunghezza del lancio misura la velocita' del corpo alla fine della
discesa. v = kL
dim1: EC = EG poiche' tutta l'en gravitazionale si
trasforma in en cinetica. EG = P*H. In totale EC = P*H.
dim2: a) La lunghezza del lancio
orizzontale e' direttamente proporzionale alla velocita' di decollo. E' la
conclusione dell'ultimo esp dell'anno di studio precedente.
b)
La velocita' di decollo si puo' ritenere uguale alla velocita' alla fine della discesa, poiche' nelle
nostre condizioni la diminuzione di velocita' nel tratto orizzontale che
porta al decollo, e' trascurabile.
Scopo. Studiare la relazione tra: l'en cinetica di un corpo, e la sua velocita'.
Il teatro operativo proposto soddisfa questo scopo, poiche' siamo in grado di
misurare entrambe: l'energia cinetica e la velocita'.
- EC . L'EC della sfera alla fine del dislivello e'
il risultato della trasformazione della sua en gravitazionale EG
all'inizio: EC = EG . EG = P*H. In totale EC = P*H.
- v.
v velocita di decollo di un lancio orizzontale e' direttamente proporzionale
alla gittata
Interpretaz energetica di v = k√H
v = k√EC siccome H misura EC . La velocita' e'
dir prop alla radice quadrata dell'en cinetica.
v2 = kEC il quadrato della velocita' e' dir prop
all'en cinetica, e viceversa, l'en cin e' dir prop al quadrato della velocita',
che e' la formula standard
|
|
|
| Ec |
Energia cinetica del pm (punto materiale) |
| M, v |
massa e velocita' del pm |
|

