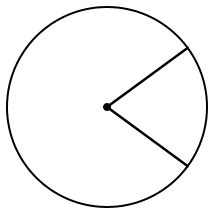
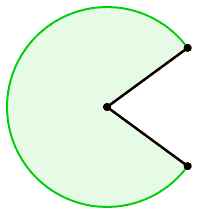
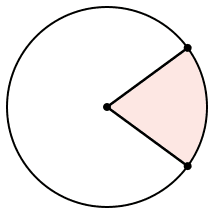
la parte di cerchio delimitata da 2 raggi.
Es materiale: una fetta di torta.
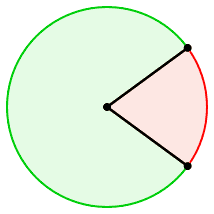
I raggi dividono il cerchio in 2 settori !
poiche' lo dividono in 2 parti:
un settore ed il suo complementare
(complementare al cerchio intero).
|
|
settore circolare
la parte di cerchio delimitata da 2 raggi. Es materiale: una fetta di torta. |
|
|
Attenz!
I raggi dividono il cerchio in 2 settori ! poiche' lo dividono in 2 parti: un settore ed il suo complementare |
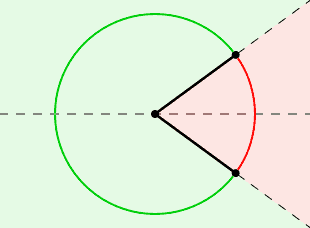
Per identifare il singolo settore, dati 2 raggi,
deve essere indicato il settore considerato
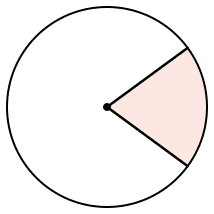
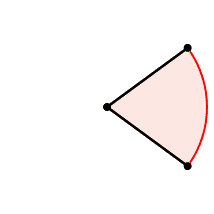
modi
di farlo.
La scelta tra 2 creati gemelli e' analoga nella definizione di:
angolo, settore circolare, arco circolare.
 |
|
immerso
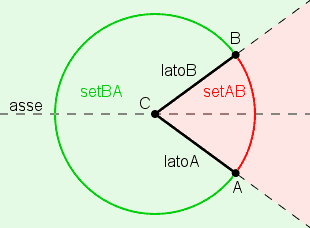
Il settore circolare ha un asse di simmetria che e' la bisettrice dell'angolo, divide il settore in 2 semisettori circolari, che sono essi stessi settori circolari.
nm ristretta: arco, corda, freccia
dando l'asse ed un lato
Diario: questo mi fa pensare che per la circonferenza un diametro e' un asse di simmetria, ed e' da dimostrare.
L'asse di simmetria divide il tri al centro (che e' isoscele) in 2 tri
rettangoli.
In trigonometria si e' scelto di usare il tri rtg come base per la descrizione,
rispetto ai tri isosceli, logicamente equivalenti, poiche' l'uso ha mostrato che
coi tri rtg e' piu' pratico nella grande maggioranza dei casi.
Di caso in caso di studio, solo una parte sono di interesse, ma ci sono sempre tutti, e forse conviene sempre cmq vederli immersi-ambientati nel settore circolare, che in questo modo da' organicita' alla visione. Principio di assimilazione: prima assimilare, e poi distinguere.
Ho la pagina Arco corda freccia in cui mi focalizzo su questo aspetto, poiche' in tanti contesti e' cio' che basta, e' il minimo indispensabile, sembra economia, e' come molta matematica e' svolta, ma alla lunga non sviluppa il pensiero creativo poiche' non stimola le connessioni, che sono soprattutto inizialmente ambientazioni.
Ho definito in locale all'arco la terminologia "corda" e "freccia", ma le ho ricopiate anche qui per avere un quadro sinottico.
data la ricchezza dell'ambiente, la terminologia e' notevole, quindi ha una pagina a se' nm.
Archi e raggi di un angolo. Settori circolari di un
angolo.
Polisettore in modo analogo a poligono.
Circonferenza passante per 2 punti. Crocevia della conoscenza.
| 1 | raggio | definisce il cerchio | ||
| 2 | arco | definisce la parte | ||
| 3 | angolo |
|
||
| 4 | corda | |||
| 5 | freccia |
Disegnare l'oscillazione del pendolo come settore circolare.
dim: si puo' dimostrare in modo statico, ma il modo che preferisco e' quello cinetico.
La figura composta dal raggio e dalla sua tangente si muove in modo rigido, quindi se l'angolo del raggio si sposta di un angolo, altrettanto si spostera' tutti gli elementi solidali.
Disegno GeoGebra crc_sector.ggb
posso o no disegnarli-considerarli e questo stimola-suggerisce considerazioni o no.
Piano come simmetrizzazione del semipiano.
Gruppo come simmetrizzazione del semigruppo.
un semipiano non e' piu' un piano, invece un semisettore e' ancora un settore.
Dato che tutto in trigonometria si svolge in un settore circolare. Cio' non appare evidente nella descrizione standard poiche' si prende come ambiente la circonferenza e poi si parla soprattutto di angolo, poiche' si studia le dipendenze dall'angolo, ma circonferenza+angolo → settore circolare.
La definizione usuale di "angolo come parte di piano" poi viene nella pratica dello studio degli angoli abbandonata poiche' tutto si svolge localmente basandosi sul cerchio trigonometrico.
cmt: 1. asimmetrica; 2. simmetrica
I 2 raggi dividono in 2 il cerchio, delimitano 2 settori di cerchio: un settore ed il suo complementare; quale sia quello compreso, cioe' quale dei 2 e' il settore considerato e' scelta del creatore.
la scelta tra 2 settori circolari
Sono molti gli elementi geometrici del settore circolare !
o
Ampiezza lineare e ampiezza angolare
sottosettori angolari di un settore angolare