^^2 variabili inversamente proporzionali. yx=k  y=k(1/x).

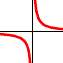
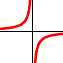
k>0   k<0

2 variabili inversamente proporzionali (=def) il loro prodotto e' costante.

Commento alla definizione

c: La versione simmetrica implicita e' usuale dei libri di matematica di scuola media inferiore. Ha lo svantaggio di non rientrare nello schema definitorio generale di "funzione". La conoscenza di questa forma simmetrica e' pero' opportuna in molti casi.

Se consideriamo la corrispondenza anche con x negativa (≡ dominio nr relativi)

	k>0 e' inversamente proporzionale decrescente
	k< 0 inv prop crescente

1. 2 variabili proporzionali. y/x=k y=kx
2. Proporzionalita' diretta e inversa di 2 grandezze variabili. Formule.
3. Proporzionalita' diretta e inversa per le funzione potenza.
4. esOf: x+y=k, x-y=k, xy=k, x/y=k.

Lg

Proporzionalita' inversa = inversa proporzionalita' =

proporzione inversa  = inversa proporzione

Esempio paradigmatico: Inversa proporzionalità dei lati di un rettangolo, con area rettangolo costante.

ref: Rettangoli equiarea.

Rpr astratta inversa proporzionalità.

2010-11 Idem per: triangolo rettangolo; parallelogramma equiarea angoli k; trilato equiarea 1 angolo k.

Scrittura in riga

y= k(1/x)

Inversa proporzionalita', come esprimere verbalmente il riconoscimento. >>>

Links

1. Variabili concordi e discordi; dipendenza concorde e discorde.

2. Variabili discordi. Caso a somma costante x+y=k x+y=0. Qui: Variabili discordi. Caso a prodotto costante x*y=k  x*y=1. Proporzionalita' inversa.

3. Se y=1/x allora dy/y = -dx/x   dy/dx = -1/x²
4. Onde in un fluido.

Approfond

xy=0  ≠  y=0/x

xy=0 inteso come equazione, ha come soluzione sia l'asse delle x che l'asse delle y.

Guida ins

Diario

Pensavo: y=1/x e', come grafico cartesiano, un'iperbole equilatera; moltiplicandone l'ordinata, e' ancora un'iperbole equilatera? se non equilatera e' ancora iperbole? Non riuscivo piu' a intravedere che la curva avesse un asse. Avevo chiesto a un collega matematico, ma ricevuto una spiega bofonchiata, per lui ovvia, ma da me incompresa nelle ragioni. Si!, diceva, semplicemente l'intersezione con un cono piu' sollevato. La ragione mi fu chiara nella risposta di Andrea Farusi: "Se l'equazione la scrivi xy=k, ti appare chiaro."

Talk

c: E' una versione che ho fatto per ricordarmi che e' simmetrica.

yx = k     versione implicita. Simmetrica.

Titolo

1. Variabili discordi. Caso a prodotto costante xy=k.
2. Proporzionalita' inversa. xy=k  y=k(1/x).
3. Proporzionalita' inversa in forma funzione.
4. 2 variabili inversamente proporzionali.
   c: mi sembra il piu' vicino all'uso dialogico in classe.
   "Proporzionalita' inversa" mi sembra piu' classificatorio.
   "Proporzionalita' inversa in forma funzione" pure. E' vero che distingue dalla forma proporzione, ma forse conviene appesantire il titolo solo al caso proporzione.

Vedere anche il discorso sul titolo di >>>

Disegno

ho ritoccato