^^Ms
coord cart punti circonferenza, in corrispondenza di prefissati angoli.
Qui misurare presentare, la' post riflessione.
Posizionare il sistema di riferimento cartesiano.
- origine degli assi nel centro del cerchio
- asse x oriz, positivo verso destra
- asse y verticale, positivo verso l'alto.
|
 |
Quali punti misurare ? (alternative)
|
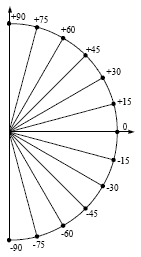
Semipiano destro, ogni 15°. R=10cm
|
 |
|
|
|
1° quadrante, ogni 10°. R = 10 cm |
|
Tutti i quadranti, ogni 15°. R = 8 cm |
 |
|
 |
|
|
|
Dimensioni.
Raggio R = 10 cm, e' grande, per cui si disegna 1/2 o 1/4
circonferenza, per stare nel foglio. Raggio R = 8 cm, se si fa tutta la circonferenza, per stare nel
foglio. Si puo' usare un disegno gia' fatto Es Dividere crc
ang 15°. |
Vincoli
- Misure in cm (e mm), usando il righello. Es 3,7,
non leggendo i quadretti. Cercare di leggere anche il mezzo mm.
- Precisione al mm. Disegnare scostandosi dalla
posizione esatta al massimo di 1mm. Chi vuole puo'
valutare a occhio anche le frazioni di mm.
- Dare un ordine: Il 1° punto viene posto
sull'asse x, all'intersezione con la circonferenza, gli altri seguono in verso antiorario.
- Nome dei punti: il valore dell'angolo,
poiche' in questo modo sappiamo immediatamente a quale angolo si riferisce
il punto. In generale si potrebbe usare la numerazione, qui a partire da 0,
o l'alfabeto, ma in questo caso non conviene.
Per i punti simmetrici rispetto all'asse orizzontale, esprimiamo la
simmetria col nome:
- angolo di segno opposto.
- Se si usano le lettere, usando la stessa lettera, con l'aggiunta dell'apice.
Es:
al punto B corrisponde B'.
- Coordinate con segno. Le coordinate y sono
positive sopra l'asse x, negative sotto.
- Organizzare i dati in tabella.
| x |
Non ho capito come si misurano le coordinate dei punti sulla
circonferenza |
|
come si fa per un qualsiasi punto del piano cartesiano. Anche se
l'attore iniziale e' la circonferenza, ora c'e' un secondo attore,
comprimario, abbiamo introdotto un piano cartesiano come sistema di
riferimento. |
Suggerimenti per non sbagliare
- Misurare entrambe le coordinate. Devono essere misurate sia la coordinata x che la coordinata y, cioe' entrambe
le coordinate, non solo 1 (una). Per ogni punto, le misure da fare sono 2: la
coordinata x e la coordinata y.
- Il disegno e' simmetrico rispetto all'asse orizzontale, quindi le
coordinate y dei punti simmetrici rispetto all'asse orizzontale, sono
opposte.
- Coordinate "meno" sotto le x. Le coordinate sotto l'asse delle x hanno il segno -
- (x;y) prima la x, poi la y. Rispettare l'ordine
delle coordinate. Nella tb coordinate: prima x, poi y.
- Coordinate uguali a 45°. L'angolo di 45° ha il punto con le coordinate uguali, poiche' e' il
vertice di un quadrato.
Es: Coordinate 45°: (5,5 ; 5,9) ERRORE ! devono essere uguali, c'e'
qualcosa che non va, da scoprire. (6,9 ; 7,2) errore !
- Angoli di 15°. Il cerchio diviso in angoli di 15°. L'angolo retto e' diviso in 6 parti,
non in un numero diverso.
- Divisione in parti uguali, non parti di diversa grandezza.
- Misurare col righello millimetrato invece che
con i quadretti, dove si sbaglia contandone 1 in piu' o in meno.
- Leggere il righello. Es 7 e 7 e' 7,7. Es
5cm 7mm e' 5,7 cm
- 1q ≠ 1cm. Quando si misura per differenza, Es 1q
agli 8 cm, sbagliare confondendo 1q con 1 cm; leggere 7 invece che 7,6. 1q =
0,4 cm = 4 mm, o 1q = 0,5 cm = 5 mm.
- Quando si copia dal sito, occorre copiare capendo. Es: le misure nel
sito possono essere piu precise di quelle misurare col righello, poiche'
sono calcolate. Se il compito e' di misurare, non si puo' copiare il
risultato.
d: Quali sono le coordinate del punto della circonferenza che sta sull'asse
delle x?
d: E quelle di quello che sta sull'asse delle y?
Come fare le tabelle ?
Dato che e' la prima volta, mostriamo come organizzare in tabella i dati
delle coordinate cartesiane dei punti del piano cartesiano. Di molti punti, ma
anche di pochi, al limite anche di 1.
Ogni 10°
|
|
Ogni 15°
|
|
Simmetrici, ogni 15°
|
|
|
|
|
|
|
| N |
β |
x |
y |
| A |
0 |
10 |
0 |
| B |
10 |
|
|
| C |
20 |
|
|
| D |
30 |
|
|
| E |
40 |
|
|
| F |
50 |
|
|
| G |
60 |
|
|
| H |
70 |
|
|
| I |
80 |
|
|
| J |
90 |
0 |
10 |
|
|
| N |
β |
x |
y |
| A |
0 |
10 |
0 |
| B |
15 |
|
|
| C |
30 |
|
|
| D |
45 |
|
|
| E |
60 |
|
|
| F |
75 |
|
|
| G |
90 |
0 |
10 |
|
|
| N |
β |
x |
y |
| A' |
0 |
10 |
0 |
| B' |
-15 |
|
|
| C' |
-30 |
|
|
| D' |
-45 |
|
|
| E' |
-60 |
|
|
| F' |
-75 |
|
|
| G' |
-90 |
0 |
-10 |
|
Qual e' la precisione dei dati misurati con righello millimetrato da 10 cm ?
1 mm e' l'errore assoluto
1/100 l'errore relativo rispetto al "fondo scala", la massima misura
possibile
Terminologia: i dati misurati col righello millimetrato sulla circonferenza
di raggio 10 cm, li chiamo misurati al centesimo, poiche' come famiglia vanno da
0 a 100 mm, e quindi il valore maggiore e' 100 volte il minore, che viene preso
come unita' di misura.
Continua
- Cioe'
misurare la corrispondenza
β → (x,y)
- C'e' cambio di coordinate. d:
Scambio valore delle coordinate, caso o regola?
- Come esprimere matematicamente
la corrispondenza di posto?
- sen cos raccolta. Per ecz numerico.
- Tb sen cos al millesimo, ogni 5°.
- Post
Arrivi
Posizioni dei punti
sulla traiettoria circolare del pendolo.
Approfond
Guida ins
Questa e' una pagina fondamentale, a cui da diversi luoghi, si
arriva a riposare.
Talk
Nome file: crc_tri = circonferenza trigonometrica
Dida
- Se e' il 1° uso delle coordinate cartesiane, accertarsi a posteriori chi
non e' capace a misurarle.
- Dichiarare la convenzione standard per il
piano cartesiano-polare.
c: Misurare le coordinate cartesiane dei punti della circonferenza.
cmt: e' un compito diverso dal farlo "in corrispondenza di determinati
angoli"
Residenza
Ott2010 alla creazione l'ho messo in "Trigonometria", poiche' ho voluto
sottolineare "in corrispondenza di prefissati angoli", dunque non coordinate a
caso, bensì "in corrispondenza agli angoli". Pero' sarebbe potuto stare in:
Didatticamente e' un esercizio che proprio per questo prende piu' piccioni
con 1 fava.
- Posizione del sistema di riferimento cartesiano
- Posizione del sistema di riferimento cartesiano
Disegn
 crc_div.xcf in
crc_div.xcf in

Alter espo
Quali punti misurare ? (alternative)
|
Semipiano destro ogni 15°
|
 |
|
|
1° quadrante ogni 10° |
 |
|
| Dove ? |
Quali ? |
- nel 1° quadrante
- nel semipiano destro
- nel semipiano superiore
- tutta la circonferenza
|
- ogni 10° = dividere
angolo retto in 9 parti uguali
- ogni 15° = dividere
angolo retto in 6 parti uguali
|

 crc_div.xcf in
crc_div.xcf in
