^^Velocita' di discesa in funzione del dislivello, con tratto orizzontale cronometrato.
pre |
fn |
in |
tit |
img |
ms |
en | cron
Analogo Velocita' di discesa in
funzione del dislivello, con lancio orizzontale.
RELAZIONE e'
- Disegno .odg|pdf.
I calcoli per disegnare la traiettoria sono in questa pagina. Si puo'
rinunciare a disegnare la traiettoria, solo i punti di impatto, con una
piccola penalita' sul voto. Il disegno della traiettoria e' gia' stato affrontato
nell'elaborato
>>>
- Misure & elaboraz .ods|pdf,
copiare pag 5 del pdf
- questa pagina (secondo le
regole).
Layout (disposizione)
per cercare di stare in 1 foglio:
faccia A: titolo, disegno, e questa pagina; dove disporre il
disegno e' a piacere.
faccia B: Misure & elaboraz.
extra: invece di copiare le misure del disegno, usare quelle dell'esp in
scala 1:10
es: altezza della gittata (del lancio) HG≡HL= 93,4 cm reali, diventano 9,34
cm nel disegno; arrotondati al mm 9,3 cm.
Il disegno di modello e' stato fatto cosi'. Siccome HG≡HL= 8,5cm nel disegno,
si puo' dedurre che il reale era 85cm.
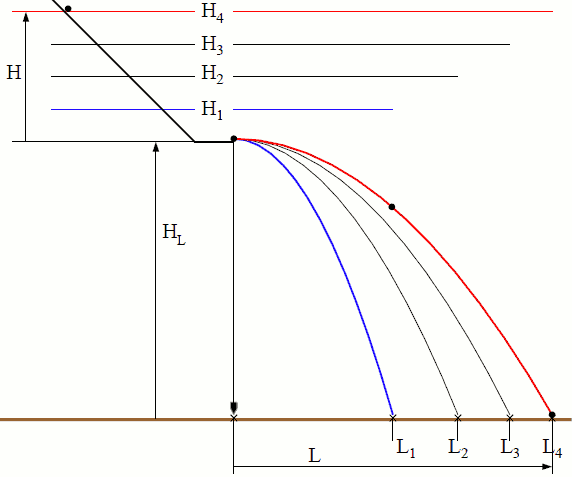
Velocita' di discesa in funzione del dislivello. (titolo teorico).
Discesa che finisce con tratto orizzontale cronometrato. (titolo operativo).
Conclu:
la velocità raggiunta in discesa
- NON è direttamente
proporzionale al dislivello
- e' dir prop alla radice quadrata del dislivello
v=k√H se H *m
⇒ v *√m
equi:
- l'altezza e' direttamente proporzionale al quadrato della velocita'
- l'energia cinetica e' dir prop al quadrato della velocita'
Si nota che H4 = 4H1 e L4=2L1

Il corpo scende: l'energia gravitazionale si trasforma in en cinetica.
- Il corpo scivola-trasla: tutta l’en cin e’ traslatoria.
- Il corpo rotola: parte dell'en cin e’ rotatoria,
di conseguenza la velocita' di traslazione è minore rispetto al caso di "sola traslazione".
Come calcolare le traiettorie per disegnarle (da non mettere in relazione)
Il disegno richiede un moto parabolico con:
- HL = 85mm altezza del lancio
- L = 49 69 85 98 mm lunghezza della gittata, di ognuno dei 4 casi.
Decidiamo di suddividere il moto parabolico in 10 fasi.
Calcoli in mm, arrotondati al mm alla fine dei calcoli, per essere tracciati.
Per fare i calcoli conviene decisamente usare il foglio di calcolo:
.ods. E' possibile riusarlo,
basta inserire i dati iniziali, e vengono forniti i risultati.
Calcoli arrotondati al mm (arrotondamento sul risultato finale)
calc Livelli della caduta
MAKv0=0 s=kt² k=0,85/100
| t |
t² |
s=kt² |
∆s |
| 0 |
0 |
0 |
1 |
| 1 |
1 |
1 |
2 |
| 2 |
4 |
3 |
5 |
| 3 |
9 |
8 |
6 |
| 4 |
16 |
14 |
7 |
| 5 |
25 |
21 |
10 |
| 6 |
36 |
31 |
11 |
| 7 |
49 |
42 |
12 |
| 8 |
64 |
54 |
15 |
| 9 |
81 |
69 |
16 |
| 10 |
100 |
85 |
// |
|
calc Moto orizzontale,
MVK s=kt k=49/10 69/10 ecc
| t |
s=kt |
∆s |
s=kt |
s=kt |
s=kt |
| 0 |
0 |
5 |
0 |
0 |
0 |
| 1 |
4.9 |
5 |
6.9 |
8.5 |
9.8 |
| 2 |
10 |
5 |
14 |
17 |
20 |
| 3 |
15 |
5 |
21 |
26 |
29 |
| 4 |
20 |
5 |
28 |
34 |
39 |
| 5 |
25 |
4 |
35 |
43 |
49 |
| 6 |
29 |
5 |
41 |
51 |
59 |
| 7 |
34 |
5 |
48 |
60 |
69 |
| 8 |
39 |
5 |
55 |
68 |
78 |
| 9 |
44 |
5 |
62 |
77 |
88 |
| 10 |
49 |
// |
69 |
85 |
98 |
|
Ottengo una traiettoria con una curvatura irregolare; voglio capire come mai
per questo ho
calcolato ∆s (anche se non serve per fare il disegno); l'approssimazione al mm
che sembra poca cosa sullo spostamento totale, provoca delle irregolarita' piu'
evidenti sui ∆s che determinano l'inclinazione del segmento di traiettoria.
Conclu: la "colpa"-causa e' l'approssimazione al mm.
Approfond
Sfera piena omogenea rotola
>>>
|
5 |
|
2 |
|
|
ECTOT = ECTRASL + ECROT =
|
|
ECTOT + |
|
EcTOT |
|
7 |
|
7 |
|
 ix Rotola sfera su guida.
ix Rotola sfera su guida.
Corsa rotolando. Momento d'inerzia.
Disegno apparato
.odg|pdf



Disegn .odg|pdf
Guida ins
zoom 66%

zoom 50%





