^^Elevazione osci pendolo, calc dall'ampiezza, col teo di Pitagora. frml

Calc l'elevazione dell'osci, dalla sua ampiezza e raggio.

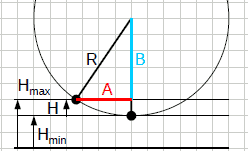
dim: H=R-B  e  B=√(R²-A²). In totale, sostituire: sostituire B in H=R-B, con  la sua espressione  B=√(R²-A²), si ottiene H= R-√(R²-A²) Spiega con aiuti .odg|pdf

Uso:

Velocita' all'estremo inferiore, ms cronometro 1 fotocellula.

Approssimazione per piccoli angoli, A/R < 0,2

Considerare triret alla circonferenza. Teo di Euclide dell'altezza A² = (2R-H)*H. Per piccoli angoli: 2R-H ≈ 2R, sostituendo: A² ≈ 2RH ;    H ≈ A²/2R

Formula in astratto geometrico: senver

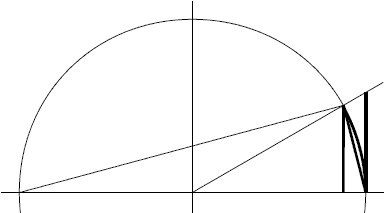analogo: Raggiometro. Arco corda freccia. frml

Approfond

Elementary view from an advanced standpoint

Approssimazione per piccoli angoli

Quello qui presentato e' un METODO ELEMENTARE di dimostrazione.

Nella nomenclatura-ambiente dell'elevazione dell'osci di un pendolo.

Nella nomenclatura astratta geometrica: senoverso

Elevazione in funzione dell'ampiezza. Calc esatto col teo di Pitagora.

Modo. y=R-radq(R²-x²)   ispezionando la geometria.

Modo. Circonferenza nell'origine: x²+y²=R². Ramo 4° quadrante: y=-√(R²-x²). Traslo verticale di +R.

Link

Guida ins

Alter espo

H= R-√(R²-A²)  ≈ A²/2R  per piccoli angoli, A/R < 0,2