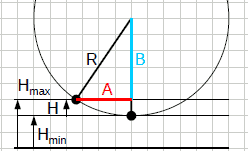
^^Pendolo; velocita' all'estremo inferiore, ms cronometro 1 fotocellula.

 tx | Er(HfA)
  dim: H= R-√(R²-A²).

 

 

 

Descrizione semplice empirica del fenomeno

Un pendolo viene sganciato, si mette in moto da v=0 fino a raggiungere la massima velocita' nel punto piu' basso.

Scopo

Ms la velocita' nel punto piu' basso, e confrontarla con la previsione ottenuta con la legge di conservazione dell'energia meccanica.

Teoria

EC= ½Mv²    energia cinetica di un PM (punto materiale)

M massa del PM; v velocita' del PM
EG= PH   energia gravitazionale di un PM

P peso del PM;
H altezza del PM rispetto ad un livello di riferimento
EG= gMH   tenuto conto P=gM; M massa PM; g gravita' =9,8 m/s²

Legge di conservazione dell'energia, adattata al caso in esame

∆EC = -∆EG  nella discesa, l'incremento di en cinetica e' uguale al decremento di en gravitazionale.

Nel caso in esame

stato1 = corpo pendolare nel punto di sgancio; v1=0; H1=Hmax≡H

stato2 = corpo pendolare nel punto piu' basso; v2=vmax≡v; H2=0 poiche' come livello di riferimento dell'altezza scegliamo il piano passante per il punto piu' basso.

∆EC = EC2 - EC1 = EC2  poiche' EC1=0 dato che v1=0

∆EG = EG2 - EG1 = -EG1  poiche' EG2=0 dato che H2=0.

In totale:  EC2  =  EG1 : l'en cin al fondo dell'oscillazione e' = all'en grav nel punto piu' alto (rispetto al fondo).

Siccome e' possibile prevedere l'en cin nello stato2, di conseguenza la velocita' !

Sostituendo le formule di calcolo

½Mv² = gMH   semplifico per M
½v² = gH     ricavo v
v=√(2gH)   velocita' finale prevista.

Esp ed elabor (E&E) (2Aele2017-22dic)

34,55 mm    Diametro sfera acciaio = spostamento di transito.
189,1 cm   R≡L raggio osci pendolo ≡ lunghezza del pendolo = dal punto di aggancio al baricentro sfera.
10 cm   Ampiezza di sgancio

Ms tempo di oscuramento-transito

ms ms ms
t_R1 t_R2 t_R3
153,3 152,6 153,2
      
ms   millisecondi
t_R1    ripetizione nr 1

Misurare H= R-√(R²-A²), e non direttamente col metro.

Misurare v

     

Prevedere v=√(2gH)

     

Confront
ms m/s
tmed v=s/t
153,03 0,2258
 
cm m m/s
H H v
0,2646 0,002646 0,2277
 
adim
D%
-0,9%

Conclu

I risultati sperimentali concordano con la teoria: i valori piu' probabili differiscono per meno dell'1%.

D: perche' misurare H= R-√(R²-A²), e non direttamente col metro ?

R:  >>> (NdR: da ricopiare).

 

 

Fine relazione da copiare.
 

Le misure utilizzate sono 2Aele2017-22dicembre, ma possono essere utilizzate anche dall'altra classe 2Ainf; se vogliono usare i propri dati di classe sono nell'approfond.

 

Leggere-osservare i dati nell'approfond, poiche'  con 2Ainf2017-22dicembre si e' riuscito a fare piu' misure, variando Ampiezza di sgancio.

 

Approfond

Per misurare H= R-√(R²-A²)

Altezza di un'osci del pendolo, calcolata dall'ampiezza, col teo di Pitagora.

Calc .ods

E%  H= R-√(R²-A²) >>>

col calcolo  H= R-√(R²-A²)  si ha come effetto della propagazione dell'errore con le operazioni matematiche E%≈2%, 20 volte meno di quello della misura diretta col metro.

 

Dis .odg|pdf

Baricentro sfera = centro sfera omogenea

lg: Esp ed elabor (E&E)

Esperimento ed elaborazione.

Esperimentare ed elaborare.

Links

  1. Esp storico (15-mag-2004) con materiale povero
    Pendolo; velocita' all'estremo inferiore
  2. esof: Energia meccanica.
  3. esof: Lancio.
  4. Discesa, trasformaz di en gravita' in en cinetica.

 

2Ainf2017-22dic

59,90 mm    Diametro sfera ottone = spostamento di transito.
190,6 cm   R≡L raggio osci pendolo ≡ lunghezza del pendolo = dal punto di aggancio al baricentro sfera = centro sfera omogenea

Ms tempo di oscuramento-transito

cm ms ms ms
A t_R1 t_R2 t_R3
10 230.7 238.2 240
20 117.7 118.2 116
30 80.2 80.2 80.1
40 60.2 60.6 60-2
      
ms   millisecondi
t_R1    ripetizione nr 1

 

Misurare v

     

Prevedere v=√(2gH)

     

Confront
ms m/s
tmed v=s/t
236.30 0.2323
117.30 0.4680
80.17 0.6848
60.67 0.9049
 
cm m m/s
H H v
0.2625 0.002625 0.2268
1.0522 0.010522 0.4541
2.3758 0.023758 0.6824
4.2445 0.042445 0.9121
 
adim
D%
2.4
3.1
0.4
-0.8

Oss: HfA altezza in funzione dell'ampiezza

H=kA² l'altezza aumenta proporzionale al quadrato dell'altezza, con buona approssimazione, fino a che A<(1/5)R.

In particolare:

se A moltiplica *2, allora H moltiplica *4.

Qui A=40cm quasi < (1/5)200cm.

 

 

 

Guida ins

Per allargarsi in divagazioni non strettamente legate all'esp, ad es Pendolo. Aspetti energetici. Energie del pendolo.

alv: "H altezza del pendolo" inteso come R≡L, invece del dislivello dell'osci  !!! (22-12-2017)  ref: Altezza delle oscillazioni.

Forse conviene cambiare denominazione ?

Calc H= R-√(R²-A²) = R(1-√(1-(A/R)²)

Errori; propagazione degli errori. Teoremi.

Dirlo

ECH0   l'en cin nel punto piu' basso, cioe' all'altezza H=0
=   e' uguale all'
EGHmax   en gravitazionale nel punto piu' alto, cioe' all'altezza max Hmax

NomeFile

  1. pend_v_punto_inf_fh
    c: originale