^^Riflessione e rotazione nel piano.

Diario

nella mia comprensione, le cose si sono svolte a partire dal piano cartesiano.

Le premesse per il nuovo passo di conoscenza che ho fatto sono:

1. Ho sempre cercato di mostrare agli allievi che:
   Le rotazioni di 1/4 di giro si rappresentano facilmente per mezzo delle coordinate cartesiane:  (a,b) → (-b,a)
2. Mi e' stato insegnato che la riflessione rispetto alla diagonale principale del piano cartesiano, si fa
   • "scambiando di posto le coordinate (del punto)":

   se un punto ha coordinate cartesiane (a,b), allora il suo simmetrico-riflesso rispetto alla diagonale principale ha coordinate (b,a), cioè  (a,b) → (b,a).

Stavo studiando le progressioni geometriche, ed ero arrivato a riguardare il Trilato dei punti medi, che risulta "invertito", ma non e' ribaltato, e' ruotato di ½ giro (equi: simmetria centrale). Cosi' pensavo rotazioni riflessioni simmetrie, e cio' mi ha richiamato un argomento-figura standard degli studi medi, i Punti simmetrici di un punto in un piano cartesiano (e gli angoli associati, otto:  ±β  ±π/2±β  π±β):

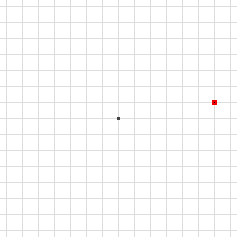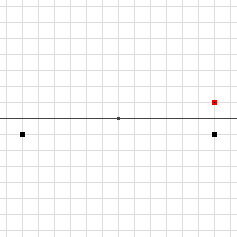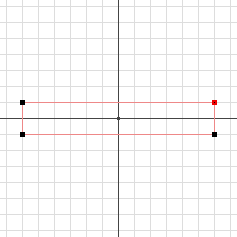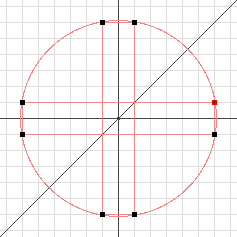clic on to animate.   La circonferenza ricorda che: simmetria assiale e centrale sono isometrie.

E qui sono accaduti 2 fatti

1. mi sono domandato:

• la simmetria rispetto alla diagonale discendente,
  come si esprime in coordinate cartesiane ?

Perche' non me lo sono domandato prima ?
Perche' non me lo hanno domandato-detto in qualita' di allievo?

2. fertilizzato dal ripensare 

    (a,b) → (b,a)  simmetria rispetto alla diagonale ascendente

    (a,b) → (-a,b) simmetria rispetto asse y

    (a,b) → (-b,a) rotazione antioraria angolo retto,

ho notato

(a,b) → (b,a) → (-b,a)

semplice, ma mai notato, e stesse perplessita' cognitive prima dette.

Controllare anche sui punti della figura a croce.

Anche simmetria rispetto all'asse x, e poi simmetria rispetto alla diagonale, produce la stessa rotazione!  (a,b) → (a,-b) → (-b,a)

Da qui mi sono ricordato che un paio di anni fa un collega mi disse che 2 ribaltamenti fanno una rotazione, e consolidato da questa info ho proseguito nei pensieri e ho concluso che l'ampiezza della rotazione prodotta da 2 riflessioni consecutive e' il doppio dell'angolo tra gli assi di riflessione.

es: ribaltamento orizzontale seguito da ribaltamento verticale = rotazione di ½ giro, si puo' leggere ora come caso particolare di una legge generale, il caso in cui gli assi di ribaltamento hanno tra loro un angolo di ¼ giro, e quindi la rotazione di angolo doppio e' proprio ½ giro.

Manca ancora da chiarire la trasformazione delle coordinate per la simmetria rispetto alla diagonale discendente, ma e' lasciata per divertimento.

Approfondimento

Esempi riflessione-rotazione

osservando la simmetria di un trilato isoscele (simmetria bilaterale rispetto alla bisettrice dell'angolo al vertice), vediamo che

• la riflessione porta un lato isoscele nell'altro;

questa trasformazione si puo' interpretare anche come

• rotazione del lato attorno al vertice, che fa centro di rotazione.

Non e' pero' una rotazione dello spazio, solo del singolo punto, poiche' ogni punto ha il suo angolo di rotazione, e il centro di rotazione si puo' scegliere ovunque sull'asse di simmetria. Questa visione serve poi ragionando sull'effetto del comporre riflessioni, in cui il centro di rotazione diventa l'intersezione degli assi di simmetria delle 2 riflessioni.

La rotazione

• ha un verso (da→a): dal lato, all'asse di simmetria;
• e' ampia il doppio dell'angolo tra il lato e l'asse di simmetria.

Per estendere il ragionamento ad una figura in generale

1. consideriamo una figura simmetrica rispetto a un lato isoscele,

   es: un gelato con lo stecco, con lo stecco al posto del lato, e il gelato che gli sta simmetricamente intorno.

   Come prima, la figura riflessa si puo' ottenere come rotazione.

2. Idem se la figura e' extra-ruotata rispetto al lato.

Se la figura non e' simmetrica, la riflessa e' "girata dall'altra parte", e' "quasi ruotata", ma girata dall'altra parte; un'altra riflessione la "raddrizzerebbe".

Fissato un asse come asse di simmetria,

se una retta interseca l'asse di simmetria, allora ...

la figura riflessa e' una retta che si puo' ottenere ruotando la retta attorno al punto di intersezione tra retta e asse.

Teo: la composizione di 2 riflessioni nel piano

• con assi paralleli, e' una traslazione.
• con l'asse di riflessione che ruota attorno a un punto,
  • e' una rotazione di angolo doppio, con lo stesso centro di rotazione.

Detto in linguaggio statico

la composizione di 2 riflessioni del piano, con assi concorrenti, e'

• una rotazione del piano attorno al punto d'intersezione degli assi,
• di ampiezza doppia dell'angolo tra gli assi.

oss: l'angolo tra gi assi in effetti sono 2: 

• β   -(π-β),  ma ...
• la rotazione e' di angolo doppio:  2β   -2π+2β 
  che differiscono  di 2π  e quindi producono lo stesso stato finale (ruotando in versi opposti).

Cartan–Dieudonné Theorem

una trasformazione ortogonale of R^n e' la composizione di al più n riflessioni.

ref: wp/Cartan-Dieudonné_theorem

D: cos'e' una riflessione in R^n ?

R: in R^2 e' riflessione rispetto a una retta, in R^n riflessionie rispetto ad un iperpiano.

Ok, ma come si definisce?

Links

brotherOf: Simmetria bilaterale. Riflessione.

Rotazioni. Punto della situazione.

esOf: Trasformazioni lineari nel piano.