^^Proporzionalita': incrementi costanti a partire da zero.

   
Stati Variazioni
x y ∆x ∆y
0 0 +3 +1
3 1 +3 +1
6 2 +3 +1
9 3 +3 +1
12 4 /// ///

D: calc y da x ?

y= (1/3)x,

y= kx 

  in generale:

k costante

x y variabili

brotherOf:  Uniformita': incrementi costanti.

esof: Proporzionalita' e uniformita', crescente e decrescente.

Costruire una corrispondenza con stati e variazioni

Guardate mentre disegno nel piano cartesiano, tratto per tratto, partendo dall'origine;
  1. asse x lungo 14q, asse y 6q
  2. traccio il punto di partenza nell'origine
  3. mi sposto a destra di 3 quadretti, ed in alto di 1q, e traccio il punto di arrivo
  4. e ripeto: mi sposto a destra di 3q, ed in alto di 1q, e traccio il punto di arrivo
  5. ripeto in tutto 4 volte

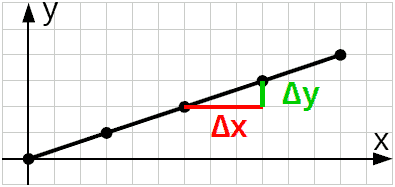
∆  :=  incremento, variazione

∆ leggesi: "delta" e' la lettera D maiuscola dell'alfabeto greco, non un triangolo, anche se la forma e' quella.
∆x leggesi: "delta x"  
∆y leggesi: "delta y"  

∆x e ∆y sono 1 in meno degli x e y, cioe' gli incrementi consecutivi sono 1 in meno degli stati, i dislivelli consecutivi 1 in meno dei livelli.

La proporzionalita' e' un caso particolare di corrispondenza uniforme.

D: Come calcolare direttamente i valori di y da quelli di x ?  ∆y da ∆x ?

          In generale:  

y

∆y

= (1/3)x

= (1/3)∆x

  

y
∆y

 = kx 

= k∆x

 k costante

x y variabili

La costante e' la stessa sia per le variabili che per gli incrementi. Cosi se la ricavo per gli incrementi (perche' piu' facile), vale anche per le variabili.

Proporzionalita' tra x e y
x e y hanno incrementi costanti a partire da zero

Proporzionalita' tra variabili. mem

Dirlo

  1. Diretta proporzionalita' tra x e y
  2. Diretta proporzionalita' tra le variabili x e y
  3. Diretta proporzionalita' tra 2 variabili
  4. variare in proporzione
  5. proporzionalitą di 2 variabili

c: Disegno, tabella, e formula per ∆x=3 e ∆y=2

Quale sara' il calcolo da fare per ottenere la y dalla x ?

Approfondimento

  1. Arrivo: Ampiezza e altezza del pendolo, ampiezza e altezza di un'osci. Lab. Ini.
    c: l'arrivo potrebbe essere qualsiasi tipo di dipendenza, quando si cerca il suo andamento.
  2. Delta ∆. | Variabile, valori, variazioni.
  3. Successione. Definizione per stati e per trasformazioni.
  4. Proporzionalita' e uniformita', crescente e decrescente.
  5. Grafico cartesiano: retta passante per l'origine.
  6. 2 variabili proporzionali. y/x=k    y=kx

Guida ins

y=⅓x  ⅓ e' troppo piccolo per una buona leggibilita'

Perche' parlare di proporzionalita' ?

E' stata citata dagli allievi, come conoscenza previa, ma e' inesatta, poiche' quasi tutti coloro che la usano, le danno il senso di dipendenza crescente.

Approfondire ?

Penso che non convenga fare un percorso sui tipi di dipendenza in astratto, bensi' chiarito che il caso di fraintendimento, continuare nello specifico. Fare solo un cenno al fatto che esistono diversi tipi di dipendenza, che si puo' presentare velocemente tramite i grafici cartesiani qualitativi.

  1. Uniformita': incrementi costanti.
  2. Proporzionalita' e uniformita', crescente e decrescente.
  3. Variabili concordi e discordi; dipendenza concorde e discorde.

 

Links

 

Spostamento obliquo scomposto in uno spostamento orizzontale e uno verticale.

Talk

Dis  .odg|pdf zoom 150%