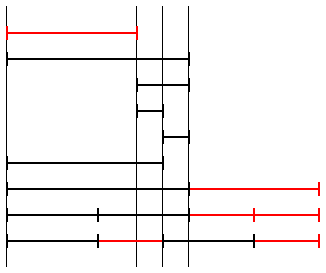
^^Intervallo su una retta. Intervallo numerico. Aritmetica dell'intervallo numerico. Centro di un intervallo.

 
intervallo come differenza di 2 segmenti

nm:

minimo    massimo    centro    ampiezza    semiampiezza ≡ raggio    (di un intervallo)

Aritmetica dell'intervallo numerico.

[x1,x2] intervallo
x1 estremo inferiore dell'intervallo. Estremo sx.
x2 estremo superiore dell'intervallo. Estremo dx.
∆x = x2 - x1 ampiezza dell'intervallo
  ∆x   x2 - x1
r = 
 = 
  2   2
raggio dell'intervallo. Semiampiezza.
c = x1 + r centro dell'intervallo
c = x2 - r  
  x1 + x2
c = 
  2
 
x1 = c - r  
x2 = c + r  

 

Incidenza di 2 intervalli, visti come 2 sfere 123D. Sfere disgiunte, sovrapposte, contenute.

Intervallo numerico vs Intervallo di un insieme ordinato.

vo: Intervallo.

Links

  1. Coord cart del punto medio di 2 punti.
  2. Centro di un segmento. Punto medio di un segmento. Centro di una coppia di punti. Punto medio di una coppia di punti.
  3. Media aritmetica di 2 numeri, 2 segmenti, 2 grandezze.
  4. Asse cartesiano, asse numerico, retta numerica. Punto rappresentativo di 1 numero; 1 variabile <-> 1 linea.
  5. Velocita' di cambiamento; andamento.
  6. Moto accelerato; come calcolare la velocita' nel moto MxK.
  7. t o ∆t ?
  8. Tempo; struttura.
  9. Intervalli; schema. | ix Intervalli e suddivisioni di un insieme ordinato.
  10. Frasi di contemporaneita'.

Guida ins

Titolo

  1. Intervallo su una retta. Intervallo numerico. Aritmetica dell'intervallo numerico. Centro di un intervallo.
    c: originale
  2. Intervallo numerico. Aritmetica dell'intervallo numerico. Centro di un intervallo.
    c: sono in dubbio se mantenere l'associazione con "Intervallo su una retta"; in effetti sembra che tutto si possa interpretare duplicemente tra algebra e Geometric Algebra.
  3. Aritmetica dell'intervallo numerico. Centro di un intervallo.
  4. Intervallo numerico, aritmetica. Centro di un intervallo.

Talk

20dic2015 tornato qui trovo questa e' la simbologia originale, che non so perche' ho usato, che ora trovo innaturale, quindi sostituisco come si vede sopra.

Forse e' interpretabile come punti e calcolo vettoriale.

 

[A1,A2] intervallo
A1 estremo inferiore dell'intervallo. Estremo sx.
A2 estremo superiore dell'intervallo. Estremo dx.
a = A2 - A1 ampiezza dell'intervallo
r = a/2 = (A2 - A1)/2 raggio dell'intervallo. Semiampiezza.
c = A1 + r centro dell'intervallo
c = A2 - r  
  A1 + A2
c = 
  2
 
A1 = c - r  
A2 = c + r  

 

 

 
l'intervallo si puo' interpretare come differenza di 2 segmenti
minimo   di un intervallo
massimo   di un intervallo
centro   di un intervallo
ampiezza   di un intervallo
semiampiezza, raggio   di un intervallo

 

minimo
massimo
centro
ampiezza
semiampiezza, raggio
di un intervallo