^^Media aritmetica di 2 numeri, 2 segmenti, 2 grandezze.

a+b     2	b-a a+   2	b-a b-   2	a   b   +   2   2
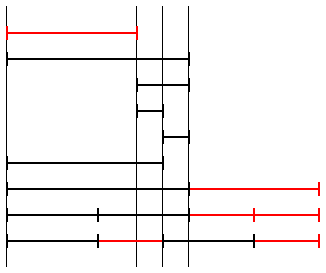
					la differenza tra i 2 segmenti si puo' interpretare come intervallo

pensiamo i segmenti siano panini di diversa lunghezza, che si vogliono compensare ad uguale lunghezza:

Media aritmetica di 2 numeri, 2 segmenti, 2 grandezze.

Come aiuto per il ragionamento, facciamo un disegno di segmenti, che si puo' intendere:

• sia in concreto, cioe' i segmenti sono-rappresentano se stessi,
• sia in astratto, cioe' i segmenti rappresentano numeri o grandezze.

Definizioni implicite di media di 2:

m-a = b-m      vuole interpretare: media equidistante da a b
m+m = a+b    media come valore uguale che sommato da' il totale

Dis .odg|pdf|png zoom75%

Links

1. Intervallo su una retta. Intervallo numerico. Aritmetica dell'intervallo numerico.
2. Centro di un segmento. Punto medio di un segmento. Centro di una coppia di punti. Punto medio di una coppia di punti.
3. Centro di N punti.

Guida ins

lg: scelta sigle. Si tratta di trovare sigle significative e non conflittuali.

Cio' che viene in mente:

Molte parole iniziano con "m"; si puo':
- usare il minuscolo/maiuscolo per distinguere es: M=maggiore m=minore
- usare sigle pluricarattere es: max min med
Scelgo le parole "piccolo" e "grande" poiche' e' significativo sia per i numeri che per i segmenti.

In occasione di una riscrittura (dic 2015) ho preferito [a,b] speso usati come estremi di intervallo. Possiamo ritenere l'ordine alfabetico a<b.

Disegno appofondito

Ho fatto tutto questo disegno approfondito per studiare con tutti i rivolti possibili la media di 2, ma forse conviene fare subito un disegno per la media di N, mantenendo cio' che vale nel caso generale.

Divisione distributiva, divisione di partizione

• partizione: pensiamo i segmenti siano panozzi di diversa lunghezza, che si vogliono compensare ad uguale lunghezza.
• distributiva: pensiamo i segmenti siano panozzi di diversa lunghezza, ognuno appartenente a una persona diversa, e che si vogliono compensare, in modo che ognuno abbia la stessa quantita'.

Raffigurare i numeri con un segmento

paragone aritmetica - geometria.

Rappresentare i nr

Dato che coi nr si rappresentano tante cose, e' possibile usare questo legame nell'altro verso: i nr sono rappresentati dalle tante cose.

1. Numeri triangolari.
2. Numerizzare tramite i numeri relativi. Usare i numeri relativi.
3. Rappresent-are/azioni; esempi.
4. La linea numerica; 1 variabile numerica <-> 1 linea.
5. Rappresentazione proporzionale delle quantita' su una linea.

Guida ins

Museo solo testo

Legenda

p    piccolo
g    grande
m    media

p    +-------------+
g    +---------------------+
g+p  +---------------------+--------------+
p+g  +-------------+----------------------+
dgp                +-------+                differenza(g,p)
dmp                +---+                    differenza(m,p)
dgm                    +---+                differenza(g,m)
m    +-----------------+
p/2  +------/------+
g/2  +----------/----------+

     +-------------+---+---+--------------+

Teo: calcolo d media aritmetica
m= p+(g-p)/2
   g-(g-p)/2
     (g+p)/2
     g/2+p/2