^^Bivettore, area; cambiamento di coordinate.

Qui vogliamo calcolare l'area del bivettore con quest'idea:

Caso semplice		Caso qualsiasi
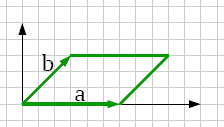1°vt collineare al 1°vt base		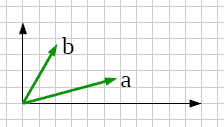vt in posizione qualsiasi

• calcolare l'area nel caso semplice
• per calcolare l'area nel caso qualsiasi:
  cambiare il sistema di riferimento, portando il caso qualsiasi nel caso semplice

Ambiente

• spazio vettoriale R²
• base ortonormale u₁ u₂
• 2 vettori: a e b
  • a= a₁u₁ + a₂u₂   ≡  (a₁,a₂)
  • b= b₁u₁ + b₂u₂   ≡  (b₁,b₂)
• a∧b  bivettore

Situazione semplice

• a∧b  ha il 1°vt colineare al 1°vt base
  cioe': a= a₁u₁ + 0u₂

di conseguenza: formula semplice

A = a₁b₂   e' l'area orientata del bivettore.

Per calcolare l'area del bvt in una posizione qualsiasi:

1. ruotare il riferimento per collineare il 1°vtbase col 1°vt del bvt
2. calcolare il cambiamento di coordinate
3. applicare la sempice formula a₁b₂ con le nuove coordinate.

Ricordo

Cambiamento di coordinate dovuto ad una rotazione.

Matrice di rotazione.

Matrice di una trasformazione lineare.

Nelle nuove coordinate

• base ortonormale u₁' u₂'
• a= a₁'u₁' + a₂'u₂'
• b= b₁'u₁' + b₂'u₂'

Per definizione-costruzione

• a∧b ha il 1°vt, colineare al 1°vt base
• a₂' = 0
• (1)  a₁' = |a| = √(a₁² + a₂²)

Cio' evita di calcolare a₁' con la matrice.

Resta da calc b₂'

(2)  b₂' = -(senβ)b₁ + (cosβ)b₂

(4)  b₂' =  (-a₂b₁ + a₁b₂)/|a|

sostituisco (3) in (2) 

A= a₁'b₂' = |a|*(-a₂b₁ + a₁b₂)/|a| = -a₂b₁ + a₁b₂ = a₁b₂ - a₂b₁ 

Caso del prodotto scalare

Per definizione-costruzione

• a·b ha il 1°vt, collineare al 1°vt base
• a₂' = 0
• (1)  a₁' = |a| = √(a₁² + a₂²)

Cio' evita di calcolare a₁' con la matrice.

Resta da calc b₁'

(2)  b₁' = (cosβ)b₁ + (senβ)b₂

(4)  b₁' =  (a₁b₁ + a₂b₂)/|a|

sostituisco (3) in (2) 

a·b = a₁'b₁' = |a|*(a₁b₁ + a₂b₂)/|a| = a₁b₁ + a₂b₂  

Approfond

Dis  .odg|pdf

Come cambia quest'espressione al cambiare del riferimento?

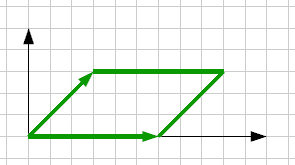
A = a₁b₂   e' l'area orientata del bivettore nella situazione semplice.

Per chiarezza meglio mettere le lettere

Talk

Penso che questo sia il modo piu' profondo di pensare al bivettore, e quindi la sua comprensione, a posteriori della genesi storica.

1 o 2 elle ?

wp/Collinearità

fr: colinéaires