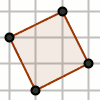
 1R: L'area del quadrato coi vertici sui nodi della griglia, e' sempre un numero
intero,
1R: L'area del quadrato coi vertici sui nodi della griglia, e' sempre un numero
intero,
Ci siamo occasionalmente accorti che se i vertici di un quadrato sono mossi sui nodi di una griglia, allora ...
Quest'idea intuitiva mi conduce ad un'indagine precisa: l'area dei triangoli.
Sempre contemporaneamente quest'idea mi fa considerare i poligoni poliquadretti .ggb
L'area dei rettangoli mi e' immediato che e' intera, e' una conoscenza base di sottofondo ai miei pensieri.
 1R: L'area del quadrato coi vertici sui nodi della griglia, e' sempre un numero
intero,
1R: L'area del quadrato coi vertici sui nodi della griglia, e' sempre un numero
intero,nonostante che:
L'area e' il suo quadrato, quindi A= c2 = a2 + b2 = intero in quanto somma di quadrati di interi.
Cmq l'area non puo' essere con la virgola con un qualsiasi numero dopo la virgola: o intera o ,5 (virgola 5).
Intuitivo: Siccome i lati vanno a coppie, c'e' sempre un doppio di mezzo, che elimina eventuali seminteri.
| .ggb | il primo casuale, che ha stimolato l'interesse. |
| .ggb | icona |
| 2.ggb | costruzione "a mano" basata sulla griglia per spiegare l'area, tramite il metodo di scomposizione |
| 3.ggb | costruzione di scomposizione, riferita alla figura, di modo che si
adatti automaticamente al variare della figura. Viene evidenziato il quadrato interno, tramite la definizione di un quadrato lý posto. Le rette sono costruite in ordine antiorario. Al variare della figura, il quadrato puo' diventare esterno. |
| 4.ggb | Invece di evidenziare il quadrato, vengono evidenziati i triangoli. |
| 5.ggb | Costruito: I rettangoli che inscatolano i lati. Appare (= Come figure non direttamente definite si notano): quadrato interno ed esterno (= quadrato inscritto, e quadrato circoscritto). Una "corona quadrata", in analogia alla corona circolare. |
a,b,c cateti e ipotenusa del triangolo rettangolo che esternamente completa a quadrato-scatola, = base e altezza dei lati del quadrato
(a+b)2 = c2 + 2ab sviluppando il quadrato: (a+b)2 = a2+2ab+b2
a2+2ab+b2 = c2 + 2ab
a2 + b2 = c2 e' il teoPitagora.
(a+b)2 = (a-b)2 + 4ab
 |
Un Quadrato coi vertici sui nodi della quadrettatura ha sempre un'area uguale ad un numero intero di quadretti. Come mai ? |