
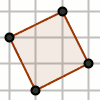
Qual e' la relazione tra l'area di una figura, ed il numero di nodi della griglia contenuti?
L'idea e' che il numero di nodi contenuti nella figura sia una buona indicazione dell'area.
E' simile al metodo della quadrettatura, solo che invece di contare i quadretti, si contano i punti
 |
I ≡ interior point, B ≡ boundary points
G. Pick
es: I + B/2 -1 = 10 + 7/2 -1 = 12,5
Area calcolata scomponendo in triangoli
6*2/2 + 3*2/2 + 3*1/2 + 1 + 1*2/2
= 6 + 3 +3/2 + 1 + 1 = 12,5
NI numero di nodi della griglia interni al quadrato, + 1, + NF nodi di frontiera contati 0,5 nel conto per l'area (non si contano i vertici).
Non vale per i triangoli, e per i poligoni in generale.
| Lato | Interni | Interni al lato | Area |
|---|---|---|---|
| 1 | 0 | 0 | |
| 2 | 1 | 1 | 1 + 1*4/2 +1 = 4 |
| 3 | 2*2 | 2 | 2*2 + 2*4/2 +1 = 9 |
| 4 | 3*3 | 3 | 3*3 + 3*4/2 +1 = 16 |
| N | (N-1)2 | N | (N-1)2 + (N-1)*4/2 +1 = ((N-1) +1)2 = N2 |

4 punti interni
0 punti sui lati
Totale: 4+1 = 5.
Possiamo anche guardare:
1 quadrato interno; 1 quadrato l'area del triangolo rettangolo la cui ipotenusa e' il lato del quadrato. Totale: 1+4 = 5.
Quadrato coi vertici sui nodi della griglia.