^^Parallelepipedo. Nomi di facce e spigoli, e loro  estensioni.

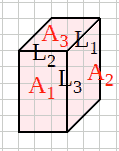
l'idea e': non dare nomi a caso, ma che "riflettano" una struttura della figura

1. Definizione nome spigoli, legata alla loro lunghezza

   L1 ≤  L2 ≤  L3 
   nome legato all'ordine: nome minore ↔ lunghezza minore
    

2. Definizione nome superfici, legata alla relaz geometrica coi nomi-spigolo

   • A1=L2xL3  A2=L3xL1  A3=L1xL2
     associazione: la faccia prodotto di spigoli ha indice seguente nella rotazione-ciclicita' 1 2 3
   • Associazione:  faccia e spigolo ortogonali hanno lo stesso indice
      

3. Teo: A1 ≥ A2 ≥ A3

   • dim1: intuitivamente,
     L1*L2 moltiplicando i 2 nr minori, ottengo il nr minore, e
     L2*L3 moltiplicalndo i 2 nr maggiori ottengo il nr maggiore.
     In stile asciutto matematico:

     A3 = L1*L2  ≤  L1*L3   ≤  L2*L3 

     poiche'           L2 ≤ L3      L1 ≤ L2

   • dim2: V = A1L1 = A2L2 = A3L3

     il volume del ppd e' sempre quello, cmq lo guardo (s-compongo AxL), quindi dall'area maggiore emerge lo spigolo minore, in modo da mantenere il volume uguale.

Esempi

Approfond

Quale nome ?

Una buona idea e' chiamarli 1 2 3, comprensibile nell'ordine in tutte le lingue.

3 facce e 3 spigoli diversi, cioe' non congruenti.

Nomi delle facce legato al nome degli spigoli

Ci sono piu' possibilita':

• Nome della faccia dato dalla composizione dei nomi  dei suoi lati.

  A12 = L1*L2   A23 = L2*L3   A31 = L3*L1

• Associazione tra giacitura e direzione ortogonali

  L1*L2 = A3   L2*L3 = A1    L3*L1 = A2

  La regola di denominazione e' formale: regola del 3° escluso, o meglio della ciclicita', per tener conto dell'ordine.

Nomi delle facce e degli spigoli, legati alle dimensioni

Nomi legati alle dimensioni, come:

• lati del rettangolo: piccolo, grande
• lati di un trilato: piccolo, medio, grande.

? Rel L1 L2 L3 A1 A2 A3

A1 = L1*L2

A2 = L1*L3

A3 = L2*L3

Guida ins

Titolo

1. Parallelepipedo. Nomi di facce e spigoli, e loro  estensioni.
   c: originale
2. Parallelepipedo. Nomi di spigoli e facce, e loro  estensioni.
   c: 16-2-2016 credo sia piu' semplice dare priorita' agli spigoli.
   Venendo da Misurare la densita' del legno di ppd (parallelepipedi) di ugual legno, sembra ovvio.

Dis .odg|pdf

originale

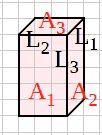
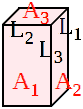
23-5-2017 zoom 50%, ritoccate in GIMP

Alter espo

Spigolo: L1 corto; L2 medio; L3 lungo. L1 ≤  L2 ≤  L3.

L1 ≤ L2 ≤ L3   A1 ≥ A2 ≥ A3