4
| C&N:
|
___-___-06 Clas_1___Geo |
| Tit: Moto uniforme e no; velocita' media, istantanea, vettoriale, segnata, assoluta; composto. | |
| 200 | Formula+invers (2p+1+1)
s=v*t |
Velocita'. Formula definitoria nel S.I. Legenda: | 20 | |||||||||||||
| - v = velocita' del moto di un punto mobile | 2 | |||||||||||||||
| - s spazio-lunghezza percorso | 3 | |||||||||||||||
| - t tempo-durata trascorso | 3 | |||||||||||||||
| U.M. S.I. m/s U.M. automobile km/ora | 2 | |||||||||||||||
| Interpretazione della formula: la velocita' numericamente e' | 1 | |||||||||||||||
| la lunghezza percorsa in 1 unita' di tempo | 2 | |||||||||||||||
| Questa e' la velocita' del mondo comune; in fisica si usa spesso anche | ||||||||||||||||
| un altro tipo di velocita': - velocita' col segno | 1 | |||||||||||||||
| che si definisce con ugual formula, ma interpretando diversamente i simboli: | ||||||||||||||||
| - s spostamento del moto, che puo' essere positivo o negativo. | 2 |
| 276 | Disegno (p2)
AAA
|
Moto relativo. Es1: A barca, B acqua, C terra | 2 | 11 |
| Es2: A passeggero, B treno, C rotaia | 2 | |||
| Formula spostamenti: sAC = sAB + sBC | 4 | |||
| Legenda: sAC= spostamento di A rispetto a C | 1 |
Come rappresentare mtm (matematicamente): a) un moto di 3 m e 2 s (3 metri e 2 secondi), e b) la sua divisione in parti uguali. Tradizionale.
| Nome(2p): Rapporto di 2 grandezze Formula(1p):
|
= |
(1p)Calcolo del rapporto unitario
|
= |
(1p)
|
3 3
1 |
7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2p) | (1p) | (2p) | (1p) | ||||||||||
| Equivalenza: | 103 m | 1 | |||||||||||
| - da U.M. pratiche |
|
|
m | ||||||||||
| per una automobile | 1 km | 103 m | 3,6*103 | 3,6 | |||||||||
| - a U.M.S.I. |
|
= |
|
= |
|
= |
|
||||||
| (p6) | 1 ora | 3,6*103 s | 3,6*103 s | 1 s | |||||||||
|
|
|||||||||||||
| 3,6*103 | |||||||||||||
| 290 | Dividere. I moti si possono dividere, cosi' come gli oggetti. | 14 | |
| Da dividere c'e': il moto e le sue 2 grandezze-quantita' : | 2 | ||
| durata T e lunghezza L | 2 | ||
| Consideriamo un moto uniforme MU. Es: caduta di una palla di carta | 1 | ||
| - dividere MU in 2 parti uguali, di conseguenza T e L | 1 | ||
| - dividere T in 2 parti uguali, di conseguenza L e MU | 1 | ||
| - dividere L in 2 parti uguali, di conseguenza T e MU | 1 | ||
| Moto non uniforme es: caduta di un sasso | 1 | ||
| - non e' divisibile in 2 parti, uguali in tutto (identiche) | 1 | ||
| - dividere T in 2 parti uguali, pero' di L generalmente diversa, moto diverso | 2 | ||
| - dividere L in 2 parti uguali, pero' di T generalmente diversa, moto diverso | 2 | ||
| 120 | Gli spostamenti lungo una linea e la loro composizione si possono numerizzare | 2 | 5 |
| tramite i numeri relativi e la loro somma. | 2 | ||
| Se hanno verso opposto, numericamente hanno segno opposto. | 1 |
| In linguaggio comune si usa dire "momento" (di tempo), in fisica puo' significare 2 cose: | 2 | ||
| un istante, una durata breve | |||
| La velocita' istantanea, cioe' associata ad un certo istante | 7 | ||
| - pratica sperimentale: e' una velocita' media di durata opportunamente piccola | 3 | ||
| centrata sull'istante considerato | 1 | ||
| - modello matematico: e' un limite, della velocita' media | 2 | ||
| facendo tendere a zero la durata | 1 | ||
| Confronto: velocita' scalare, vel vettoriale. Nel moto circolare uniforme | 2 | 4 | |
| la velocita' scalare e' costante invece la velocita' vettoriale varia | 2 | ||
| 263 | Se la velocita' vettoriale ha intensita' costante, allora | 1 | 10 |
| il moto e' uniforme. | 2 | ||
| Se la velocita' vettoriale ha direzione costante, allora | 1 | ||
| la traiettoria e' retta. | 2 | ||
| Se la velocita' vettoriale e' costante, allora il moto e' rettilineo uniforme, | 3 | ||
| poiche' e' costante la direzione e la velocita' scalare. | 1 |
Extra. Come rappresentare mtm: (1) un moto di 3 m e 2 s e(2) la sua divisione in parti uguali. Alter.
|
|
= |
|
= |
|
1 2
1 |
4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 136 | I moti si possono comporre, cosi' come gli oggetti. Le 2 composizioni fondamentali sono: | 7 | |
| 1: comporre in sequenza temporale | 1 | ||
| 2: comporre in contemporanea | 1 | ||
| es1: un passo dopo l'altro; una fermata dopo l'altra | 2 | ||
| es2: l'oggetto lanciato in avanti: mentre va avanti, intanto scende | 3 | ||
| 137 | Misura-grandezza del moto composto. Si ottiene un moto in cui: | 10 | |
| 1a: spostamenti e durate si sono sommati | 3 | ||
| 1b: la velocita' e' intermedia | 2 | ||
| 2a: spostamenti e velocita' si sono sommati | 3 | ||
| 2b: le durate sono le stesse | 2 | ||
| La legge oraria del moto uniforme. Formula: s= v*t | 1 | 6 | |
| Legenda: - s, t variabili correlate | 1 | ||
| - v velocita' costante | 1 | ||
| A parole: lo spazio percorso e' direttamente porporzionale al tempo trascorso | 3 | ||
| 140 | In fisica una variabile scalare e' raffigurata tramite una linea. | 1 | 3 |
| Segno-significato: punto-valore, spostamento-variazione | 2 |
| 200 |
∆z = z2-z1
Dz = z2-z1 Predittiva: z2 = z1+∆z
p4(=2+2) |
- z una generica variabile | 2 | 13 |
| - ∆ delta, D greca maiuscola, simbolo della variazione | 3 | |||
| - ∆z, Dz variazione della variabile z | 2 | |||
| - z1 valore iniziale | 1 | |||
| - z2 valore finale | 1 | |||
Massa, peso, inerzia, quantita' di materia; densita', rapporto.
Commenti
| Moto di un punto: direzione del moto costante corrisponde a: traiettoria retta | |||
| Il moto con una direzione costante genera una traiettoria retta. | |||
c: "direzione del moto" e' un'espressione del mondo comune. Se volessimo formalizzarlo in fisica, sarebbe la direzione della velocita' vettoriale. Rimanendo nei TT Termini Tecnici, tanto vale usare solamente "direzione della velocita' vettoriale".
| Interpretazione della formula: la velocita' numericamente e' | 1 |
| la lunghezza percorsa in 1 unita' di tempo | 2 |
c: precisando: lo e' se il moto e' uniforme.
| 467 | Quantita' e qualita' | ||
| Una grandezza e' una quantita' o una qualita' non in assoluto, ma | |||
| relativamente alla composizione considerata. |
| Le variazioni di una variabile scalare e la loro composizione si possono numerizzare | 2 | 5 | |
| tramite i numeri relativi e la loro somma. | 2 | ||
| Se hanno verso opposto, numericamente hanno segno opposto. | 1 |
| L'esempio solito di fenomeno ciclico in fisica e' il moto circolare uniforme. | 2 | ||
| Osserviamo il fenomeno ciclico per N cicli per una durata complessiva t. | 9 | ||
| frequenza f= N/t numero di cicli in 1 unita' di tempo | 3 | ||
| periodo T = t/N durata di 1 ciclo | 3 | ||
| Relazione tra frequenza e periodo: f*T=1 f=1/T T=1/f | 3 | ||
| 300 | "Allungamento forzato uniforme", visto come corrispondenza: | 4 | |
| a variazioni uguali di forza, | 2 | ||
| corrispondono variazioni uguali di lunghezza. | 2 | ||
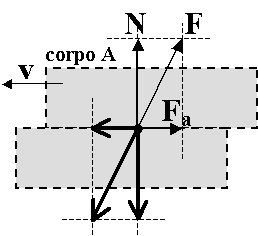
| 468 | Legge della forza di attrito statico | 1 | 14 |
| 0 ≤ F ≤ FMAX La forza F di attrito statico puo' variare da 0 a un valore max, | 4 | ||
| superato il quale il corpo viene messo in moto. | 2 | ||
|
FMAX =k* N la forza di attrito statico massima FMAX o forza di stacco, |
5 | ||
| e' direttamente proporzionale alla forza normale N | 2 |
| 332 | Nell'allungamento elastico, consideriamo la variazione della forza invece della forza | 1 | 2 |
| e la variazione di allungamento invece dell'allungamento | 1 | ||
| 2100 | Cosi' come a valore corrisponde valore, a variazione corrisponde variazione | 1 | |
| 320 | Il "sovrappeso" del linguaggio comune, interpretato come TT fisico | 2 | |
| variazione di peso DP rispetto a un peso di riferimento |
 |
 |
2
4 |
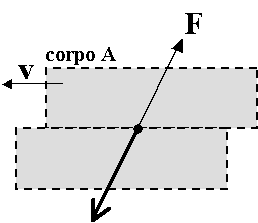
| 234 | Situazione: 2 corpi a contatto, fermi o in moto relativo | 1 | 9 |
| Es per fissare le idee: 2 corpi solidi che scivolano uno sull'altro | 1 | ||
| Disegno d risultante delle forze di contatto distribuite sulla superficie | 2 | ||
| Legenda = F risultante delle forze subite dal corpo A | 1 | ||
| Convenzione: il punto di applicazione delle forze e' nella coda | 1 | ||
| Osserviamo: - ognuno dei 2 corpi subisce e fa una forza di contatto | 1 | ||
| - una l'opposta dell'altra, come detto nel principio di azione e reazione | 1 | ||
| In questo caso: sono una coppia repulsiva | 1 | ||
| 330 | Legge della forza elastica, espressa con le variazioni. In simboli, a parole, UMSI. | 3 | |
| DF= -k*Dx la variazione di forza e' direttamente proporzionale | |||
| alla variazione dell'allungamento. N=(N/m)*m | |||