^^Approssimazioni per piccoli angoli.

La relazione si intende numerica, unita' di misura tralasciate

angolo in radianti

angolo = arco  se R=1

Approssimativamente uguali

La 2ª terna pitagorica 5 12 13  mostra come  l'ipotenusa aumenti di poco rispetto al lato lungo, confrontando l'aumento del lato corto.

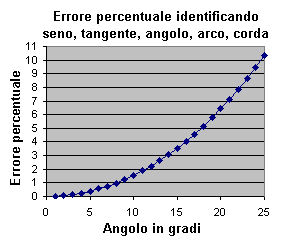.xls   Angolo < o Tangente < errore < 1° 0,02 0,02% 5° 0,1 0,4% 10° 0,2 2% 20° 0,35 6%

Guardare l'articolo su wikipedia http://en.wikipedia.org/wiki/Small-angle_formula

senβ approximation .ods

Il vantaggio dell'ultima approssimazione e' che e' cos(βMax/2) e' costante

dim: senβ = 2sen(β/2)*cos(β/2) <≈ 2β/2*cos(β/2 =  βcos(β/2)

Links

1. Angolo approssimato tramite spostamenti cartesiani; base e altezza.
2. Circonferenza approssimata con una parabola.
3. esOf: Approssimare.

Approfond

Le approssimazioni per piccoli angoli sono legate alle

Approssimazione di Gauss per l'ottica.

wp/Gaussian_optics is a technique in geometrical optics that describes the behaviour of light rays in optical systems by using the paraxial approximation, in which only rays which make small angles with the optical axis of the system are considered.

• In this approximation, trigonometric functions can be expressed as linear functions of the angles.

Talk

Titolo

1. Seno, tangente, angolo, arco e corda uguali in prima approssimazione, per piccoli angoli.
   c: originale.
2. Approssimazioni per piccoli angoli.
   c: 2giugno-2020. E' il titolo col quale cercavo la pagina, e quindi l'ho cambiato, anche perche' mi sembra troppo lungo.
3. Misura approssimata per piccoli angoli.