

Il prodotto vettoriale, di 2 vettori, A e B, AxB
| intensita' | |AxB| = |A|*|B|*sen(^AB) = AN*B = A*BN (Notazione >>>) |
| direzione | AxB ^ A e AxB ^ B il prodotto vettoriale e' ortogonale ai suoi fattori |
| verso | A, B, AxB e' una Terna destra. | Regola della mano destra. |


Source: http://serge.mehl.free.fr/chrono/Gibbs.html
AxB = AxBN = ANxB
nxB = BN componente di B perpendicolare a n, ruotata di 90° antioraria attorno al versore di rotazione n che individua l'asse di rotazione.
BP+nxB = (B∙n)*n + nxB = rotazione del vettore B di 90° antioraria attorno al versore di rotazione n che individua l'asse di rotazione.
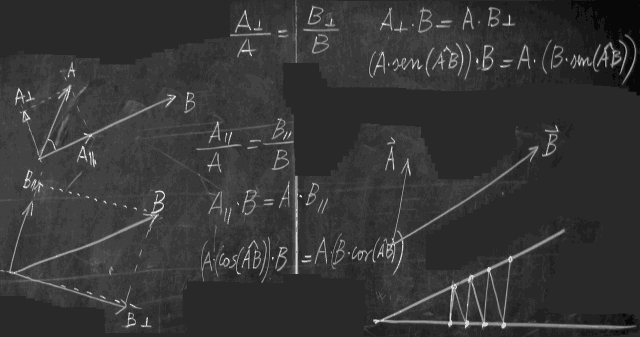
| AxB=0 ⇔ A=0, o B=0, o A parallelo B |
legge di annullamento del prodotto |
| k(AxB) = (kA)xB = Ax(kB) | prodotto per uno scalare. In particolare: |
| -(AxB) = (-A)xB = Ax(-B) | prodotto per -1 |
| Ax(B+C) = AxB + AxC | distributiva destra |
| (A+B)xC = AxC + BxC | distributiva sinistra |
| BxA = - AxB | antisimmetrico, o anticommutativo. In particolare non e' commutativo. |
Forza magnetica su una corrente elettrica F=IxB*L.
dim: AxB = Ax(BN+BP) = AxBN + AxBP = AxBN + 0 = AxBN
AxB = (AN+AP)xB = ANxB+APxB = ANxB+0 = ANxB
Il prodotto vettoriale in tal caso e' sempre perpendicolare al piano, diciamo xy, cioe' lungo l'asse z. Puo' essere quindi rappresentato da un numero relativo. Dato per scontato che la terna di riferimento sia destra, AxB e' positivo se l'angolo da A a B e' antiorario.
e' di costruire un'algebra geometrica.
Da un altro punto di vista: partendo dal modo euclideo di fare le dimostrazioni, la possibilita' di scrivere con un simbolo le varie operazioni-costruzioni che si vanno facendo, e poi la possibilita' di operare sui simboli con regole di manipolazione che producono cose sensate.
Torcente di un braccio-forza. Definizione vettoriale.