1687 Isaac Newton publishes his Principia Mathematica, in which he lays out his version of an idea that was attaining currency at that period, the idea of a parallelogram of forces. His statement is
Principia. Corollario 1. "Regola del parallelogramma".
Newton did not have the idea of a vector. He was, however, getting close to the idea, which was becoming common in that period, that forces, because they have both magnitude and direction, can be combined, or added, so as to produce a new force.
1835 Giusto Bellavitis publishes his first exposition of his system of equipollences
1840 Grassmann completes the writing of his Theorie der Ebbe und Flut (Theory
of the Ebb and Flow) and submits this 200+ page essay as evidence of his
competence for teaching. This work on tidal theory contains the first system of
spatial analysis based on vectors and is reasonably close to the modern system.
Grassmann dated the origin of these ideas to 1832 and traced his fundamental
idea to reflections on negative numbers and to the idea of adding and
subtracting directed lines. He traced his idea of a geometrical product to
textbooks written by his father and entitled Raumlehre (Space Theory) and
Trigonometrie, the first having been published in 1824, the latter in 1835. In
particular, his father had written in 1824: “The rectangle itself is the
true geometrical product, and the construction of it ... is really geometrical
multiplication.” H. G. Grassmann’s work did not come out of the geometrical
representation of complex numbers tradition; in fact, he learned of that
representation only in December, 1844.
Comment: Grassmann’s 1840 Theorie der Ebbe and Flut presents among other matters
the addition and subtraction of lines (strecken) and also what is numerically
equivalent to the modern cross product, with this difference that whereas the
product of two vectors in the modern system is another vector, in Grassmann’s
system it is a geometrical entity, the directed area of the parallelogram
between the two strecken or vectors. Grassmann also presents in this treatise
the “linear product” of two strecken, this being identical to the modern dot or
scalar product. He also treated vector differentiation.
1871 in his famous paper of 1871 titled “On the Mathematical Classification of Physical Quantities,” Maxwell states: “The invention of the calculus of Quaternions is a step towards the knowledge of quantities related to space which can only be compared for its importance, with the invention of triple coordinates by Descartes.
Dans l'addition géométrique des nombres complexes, Argand est amené à poser la formule:
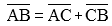
C'est la formule dite de Chasles. Argand annonce ainsi l'entrée en scène de la notion de vecteur : il voit dans les nombres imaginaires (nombres dits complexes depuis Gauss ) des lignes dirigées : segments orientés du plan : c'est bien, là encore, le point de vue de Wessel.
Ce concept, déjà présent chez Stevin au 16è siècle, se rencontrera implicitement dans les travaux de Möbius et de Chasles mais principalement et plus formellement avec Bellavitis (dans sa théorie des équipollences) et ses contemporains Hamilton, à qui l'on doit d'ailleurs l'appellation vecteur, et Grassmann. Le calcul vectoriel verra son plein essor avec les travaux novateurs de Gibbs.
La notation fléchée >>>
Source: serge.mehl.free.fr/chrono/Argand.html
Source: serge.mehl.free.fr/chrono/Hamilton
On doit à Hamilton le terme vecteur (1846), dans un complément de son premier traité sur les quaternions publié dans le journal de mathématiques de Cambridge et Dublin (The Cambridge and Dublin Mathematic Journal, 1846). Dans sa seconde édition de 1853, avant d'introduire les quaternions, Hamilton développe le calcul vectoriel.
On y voit aussi apparaître la notion de scalaire x = AC/AB lorsque A, B et C sont colinéaires. Pour nommer un vecteur, équivalent à un triplet de l'espace, il utilise les lettres grecques minuscules α, β, ... Toutes les propriétés équivalentes à la définition d'un espace vectoriel sont énoncées, comme la distributivité de la multiplication scalaire par rapport à l'addition. Propriétés également introduites d'un point de vue géométrique (sans rapport avec les quaternions) la même année par Grassmann en Allemagne.
Précisons, en toute justice et reconnaissance de paternité, que le concept de vecteur était implicitement utilisé depuis Argand dans sa représentation géométrique des nombres complexes. Le terme provient du latin vector = qui transporte. Kepler, auparavant, l'utilisa en astronomie sous la forme de rayon-vecteur, qui fut repris ensuite couramment dans l'usage des coordonnées polaires.
Calcolo delle equipollenze. 1832 Giusto
Bellavitis (1803-1880).
http://serge.mehl.free.fr/chrono/Hamilton.html
http://serge.mehl.free.fr/anx/vecteur.html
http://serge.mehl.free.fr/anx/vect_p.html
El paso siguiente lo da Hamilton. Con Hamilton inicia el estudio de los vectores. Se le debe a él el nombre de 'vector' producto de la creación de un sistema de números complejos de cuatro unidades, denominado "cuaterniones'', muy usados hoy en día para el trabajo con rotaciones de objetos en el espacio 3D. Actualmente, casi todas las áreas de la física son representadas por medio del lenguaje de los vectores.
| Bellavitis | bipunti |
| Laisant | droites limitées |
| Hamilton | vectors |
Our modern scalar and vector products arose not on principle or from
conscious desire, but rather from the practice among quaternionists of using
separately the scalar and vector parts of the full quaternion
product.
ref: Ten “Laws” concerning patterns of change in the history of mathematics - Crowe. pag3
Notwithstanding the efforts which have been made during more than half a
century to introduce Quaternions into physics the fact remains that they have
not found wide favor.
On the other hand there has been a growing tendency especially in the last
decade toward the adoption of some form of Vector Analysis.
ref: Vector Analysis: A Text-book for the Use of Students of Mathematics and Physics 1901 J.W. Gibbs - Wilson
https://archive.org/ borrow