 Disegn .odg|pdf
Disegn .odg|pdf| v = √(2g∆H) | v0 =0 | Formula per la velocita' in funzione del dislivello. |
| Per calcolare la velocita' alla fine del dislivello, occorre tenere presente come l'en cinetica si ripartisce tra en cin di traslazione e rotazione. |
|
v = √(2g∆H)*√k |
k e' la frazione di en cin traslatoria ECTRASL = k*EC k = 5/7 per una sfera omogenea che rotola senza strisciare. |
Prosegue Lunghezza gittata.
Si puo' calcolare-prevedere la velocita' alla fine della discesa.
Esistono piu' dimostrazioni, una piu' cinematica, e una piu' dinamica.
Si, ma non e' l'aspetto essenziale, poiche' per considerazioni energetiche, la velocita' alla fine della discesa e' indipendente dalla traiettoria.
1) la velocita' alla fine del dislivello e' indipendente dalla traiettoria.
2) Basta quindi risolvere in un caso di traiettoria-moto che so calcolare: la
caduta verticale, che e' un MAK.
La velocita' alla fine del dislivello-discesa e' la velocita' finale di un MAK
|
v | velocita' di un MAK con v0 = 0 | ||||||
|---|---|---|---|---|---|---|---|---|
| a | accelerazione | |||||||
| s | spazio percorso |
Nel caso scelto di caduta verticale: a=g e s=
|
v | velocita' a fine discesa con v0 = 0 | ||||||
|---|---|---|---|---|---|---|---|---|
| g | accelerazione di gravita' | |||||||
| ∆H | dislivello, altezza della discesa |
L'accelerazione sul piano inclinato e'
|
a | accelerazione sul piano inclinato | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| g | accelerazione di gravita' | ||||||||||
| H | altezza del piano | ||||||||||
| L | lunghezza del piano |
che sostituendo porta alla stessa formula finale.
EG → EC l'en gravitazionale si trasforma in en cinetica.
∆EC = - ∆EC l'incremento di EC e' = decremento di EG
EC2 = EG1 l'EC finale e' uguale all' EG iniziale, precisando che:
EG1 = P*H1 P peso del corpo, H1 altezza di sgancio sulla discesa
ECTRASL = k*EC il resto della frazione e' EC rotatoria.
| 5 | |||
| ECTRASL = |
|
L'EC di traslazione e' 5/7 della totale, | |
| 7 | 2/7 sono di EC rotatoria. |
| 2ECTRASL | ||
| v = √( | ) | |
| M |
| 2ECTRASL | 2kEC2 | 2kEG1 | 2kPH1 | |||||
| v = √( |
|
) = √( |
|
) = √( |
|
) = √( |
|
) |
| M | M | M | M |
| = √(2gkH1) | = √k√(2gH1) |
Prosegue
Per farlo seguiamo 2 "salti" della sfera:
| H | s | t | v | v = at |
|---|---|---|---|---|
| H1 | s1 | t1 | v1 | v1 = at1 |
| H4 = 4H1 | s4 = 4s1 | t4 = 2t1 | v4 = 2v1 | v4 = at4 |
| H | s | t | v | v = at |
|---|---|---|---|---|
| H1 | s1 | t1 | v1 | v1 = at1 |
| H4 = 4H1 | s4 = 4s1 | t4 = 2t1 | v4 = 2v1 | v4 = at4 |
MAK e' il moto di discesa, per cui:
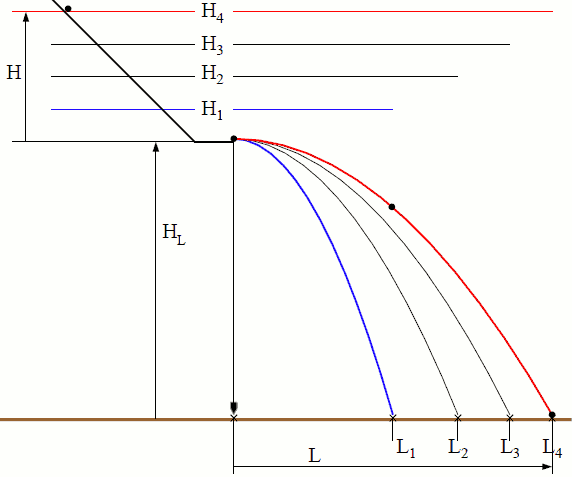
In essenza: H → v → L l'altezza della discesa causa una velocita' di fine discesa, che e' anche velocita' di lancio, che causa una gittata.
L = k√H e' la formula
| LT = 2√(H1H2) | Traslare; Scivolata senza attrito. EG → ECTRASL tutta
l'en gravitazionale si trasforma in en cinetica di traslazione, eq H1 altezza discesa; H1 altezza decollo |
| L = LT*√k | Rotolare. La velocita' alla fine della discesa |
per
rotolare k <1. Sfera omogenea rotola senza strisciare k=5/7.
Cerchiamo un ragionamento piu' semplice che ci faccia capire oltre la formula.
R: MAK ½t¼s 2t4s e' il moto sul piano inclinato. Quindi la domanda diventa ...
D: Con che velocita' il corpo arriva alla fine di un MAK?
R: v = √(2as). Questa e' la formula. Ragioniamo anche coi casi particolari: ½t¼s 2t4s ¼s½t 4s2t. Se lo spazio s e' percorso in un tempo t , allora lo spazio 4s e' percorso in un tempo 2t, e siccome nel MAK la velocita' e' proporzionale al tempo, anch'essa raddoppia.
Spazi uguali sul piano inclinato corrispondono a dislivelli uguali, quindi quello appena detto per gli spazi, vale anche per i dislivelli: dislivello 4* (4 per, cioe' moltiplicato per 4) causa velocita' 2*, dislivello 9* causa velocita' 3*.
Combinando la dipendenza del punto precedente H → v, con la presente v → L, in totale: H → v → L. Dislivello *4 causa gittata 2*.
| cm | ||||
|---|---|---|---|---|
| N | H | t | v=at | L |
| 1 | H | t | v | 49 |
| 2 | H*2 | t*√2 | v*√2 | 69 = 49*√2 |
| 3 | H*3 | t*√3 | v*√3 | 85 = 49*√3 |
| 4 | H*4 | t*2 | v*2 | 98 = 49*2 |
√2 = 1,414
√3 = 1,732
|
|
|
|
2B_2012_8_novembre
Foglio di calcolo 2012.ods
La lunghezza del lancio orizzontale e' direttamente proporzionale alla velocita' di decollo. E' la conclusione dell'ultimo esp dell'anno di studio precedente. Quindi in questo contesto, la lunghezza del lancio deve essere interpretata come un indice proporzionale della velocita', come l'allungamento della molla e' un indice della forza che fa-subisce.
l'altezza della discesa e' direttamente proporzionale all'en cinetica alla
fine della discesa.
Dimostrazione: 1) EG = P*H; 2) EG → EC l'en
gravitazionale si trasforma tutta in en cinetica.