^^Ampiezza e raggio osci.

<<<  >>>

Combinazioni di Ampiezza e Raggio dell'oscillazione.
2 valori di Raggio combinati con 2 valori di Ampiezza.

         

Esiste il problema di fare TUTTE le combinazioni.

Esiste il problema di Disporre le combinazioni.

Questa e' la disposizione a tabella.

Esiste Combinazione a piu' di 2 valori.

c: Fare tutte le combinazioni di ampiezza e raggio, con piu' valori; invece no, per semplicita' fare: Tabella di combinazione in rettangoli.

Disegnare per evidenziare le dimensioni di Ampiezza e Raggio

    con maggiore o minore successo.

Per chi guarda si tratta anche di abituarsi.

Tb combinaz, con valori e nomi delle coordinate

      

R

a

g

g

i

o

  R = 5 
 R = 2
    A = 1 A = 1,5
    Ampiezza
Vieni fuori a mostrare i casi con il tuo pendolo, realizzandoli.
  Precisi ?
  Basta che siano rispettate circa a occhio le proporzioni.
  L'allievo esegue.

cc: Disegnare. Non rinunciare a disegnare ! Cavarsela approssimando, semplificando.

Approfon

Rettangolo Ampiezza-Raggio evidenziato

Allievi indagando

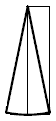
  quando il filo e' piu' lungo, l'ampiezza dell'osci e' maggiore
Non e' detto, guarda, te lo mostro maneggiando il pendolo ...

Ora tu disegna alla lavagna.
alto e stretto, basso e largo
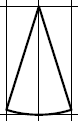
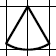
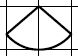
  Come si chiamano in geometria queste figure ?

Come si possono descrivere ? A cosa somigliano ?
  hanno una base curva
  somigliano a un triangolo isoscele

In geometria queste figure si chiamano settore circolare

dida: 1B_2013 1/17 lo sapeva

 

Talk

Titolo

Combinare Ampiezza dell'oscillazione e Lunghezza del filo

 

Studio espo

 

 

      

R

a

g

g

i

o

  R = 5 
 R = 2
    A = 1 A = 1,5
    Ampiezza  osci

 

      

R

a

g

g

i

o

  R = 5 
 R = 2
    A = 1 A = 1,5
    Ampiezza  osci

 

Visione osci disturbata (???) dalle righe

    Esiste il problema di fare TUTTE le combinazioni.

Esiste il problema di Disporre le combinazioni.

Questa e' la disposizione a tabella.

Esiste Combinazione a piu' valori.

c: Fare tutte le combinazioni di ampiezza e raggio, con piu' valori; invece no, per semplicita' fare: Combinazione dei rettangoli.

Per semplicita' facciamo una rappresentazione piu' astratta: la combinazione di lati che costruisce rettangoli.

 

    Esiste il problema di fare TUTTE le combinazioni.

Esiste il problema di Disporre le combinazioni.

Questa e' la disposizione a tabella.

Esiste Combinazione a piu' valori.

c: Fare tutte le combinazioni di ampiezza e raggio, con piu' valori; invece no, per semplicita' fare: Combinazione dei rettangoli.

Per semplicita' facciamo una rappresentazione piu' astratta: la combinazione di lati che costruisce rettangoli.