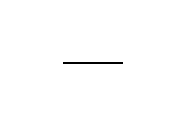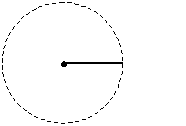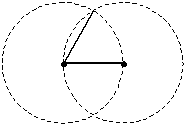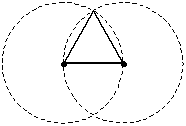^^Tri equi; trilato equilatero, la costruzione di Euclide.

Costruire un triangolo equilatero, dato un lato.

Img e parole

		dato un lato
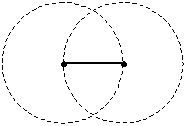
		circonferenza con centro su un estremo raggio uguale al lato (possibile per il postulato 3)
		idem con centro sull'altro estremo del lato
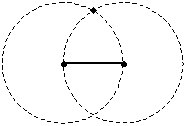
		le 2 circonferenze si intersecano in un punto (affermazione senza giustificazione >>>) (in effetti si intersecano in 2 punti, ma per rispondere alla richiesta ne considera solo 1)
		congiungere con segmenti il punto-intersezione e gli estremi del lato. (postulato 1)

Solo img

Sintesi con costruzione animata e figura finale

Nota storica

e' la prima proposizione-costruzione-dimostrazione degli "Elementi di Geometria" di Euclide.
Discende direttamente dai 5 postulati.

Dimostrazione (solo parole, come solito)

costruzione: richiede 3 passi

1. circonferenza con
   • centro su un estremo del lato, e
   • raggio uguale al lato
2. idem con centro sull'altro estremo del lato;
   le 2 circonferenze create si intersecano
3. congiungere con segmenti il punto-intersezione e gli estremi del lato.

Dimostrazione che la costruzione soddisfa la richiesta

1. un segmento aggiunto e il lato dato
   • sono raggi della stessa circonferenza
   • quindi sono uguali per definizione Euclide def15
2. quindi entrambi i segmenti aggiunti sono uguali al lato dato
   • segue dal punto precedente applicato ad entambi.
3. quindi i segmenti aggiunti sono uguali tra loro
   • segue dalla LOGICA comunemente accettata nelle dimostrazioni matematiche:
     • cose uguali ad una fissata, sono uguali tra loro.
       Euclide. Nozioni comuni 1.
4. quindi lato e lati aggiunti sono uguali tra loro,
   cioe' il trilato e' equilatero. Euclide def20

Le costruzioni di Euclide, a volte usano assiomi impliciti

• no axiom about the intersection of circles

so he has not justified the existence of the intersection of circles used in his very first proposition! >>>

Link

1. Segmento raggio di due cerchi; ani.
2. Bilobo e trilobo di Euclide.
3. Cerchi esagono. | Triangoloide; ani.
4. Dividere la circonferenza in parti uguali.

Approfond DIRLO

Dirlo

1. Costruire un triangolo equilatero, dato un lato.
2. Costruire un triangolo equilatero, dato il lato.

Dirlo

1. se cose sono uguali ad una fissa che fa da riferimento,
   allora sono uguali tra loro
2. cose uguali ad una fissata, sono uguali tra loro.

Dirlo

le 2 circonferenze create si intersecano,

1. dal punto di intersezione disegnare i segmenti che vanno agli estremi del lato.
2. congiungere con segmenti punto-intersezione con gli estremi del lato.
3. congiungere con segmenti punto-intersezione ed estremi del lato.
4. congiungere con segmenti il punto-intersezione e gli estremi del lato.
5. congiungere (con segmenti) il punto-intersezione e gli estremi del lato.
6. congiungere il punto-intersezione e gli estremi del lato.

Dirlo

costruzione: richiede 3 passi

1. circonferenza con centro su un estremo e raggio uguale al lato
2. idem con centro sull'altro estremo
3. le 2 circonferenze create si intersecano, congiungere con segmenti il punto-intersezione e gli estremi del lato.

VS

1. circonferenza con centro su un estremo e raggio uguale al lato
2. idem con centro sull'altro estremo;
   le 2 circonferenze create si intersecano
3. congiungere con segmenti il punto-intersezione e gli estremi del lato.

Dirlo. Dimostrazione che la costruzione soddisfa la richiesta

1. il lato-segmento dato e' raggio di entrambe le circonferenze
2. un segmento aggiunto e' uguale a quello dato poiche' entrambi sono raggi della stessa circonferenza
3. quindi entrambi i segmenti aggiunti sono uguali a quello dato,
   quindi sono uguaii.

VS

1. un segmento aggiunto e il lato dato, sono raggi della stessa circonferenza
   • quindi sono uguali per definizione Euclide def15e16
2. quindi entrambi i segmenti aggiunti sono uguali al lato dato
   • segue dal punto precedente applicato ad entambi i segmenti aggiunti.
3. quindi i segmenti aggiunti sono uguali tra loro
   • segue dalla LOGICA comunemente accettata nelle dimostrazioni matematiche:
     • cose uguali ad una fissata, sono uguali tra loro. Euclide. Nozioni comuni 1.
4. quindi lato e segmenti aggiunti sono uguali tra loro, cioe' il trilato e' equilatero.

Approfond

Disegno-studio costruzione .odg|pdf

Talk

Vecchia versione

Veloce

Singole img

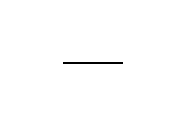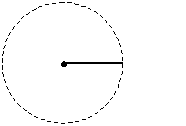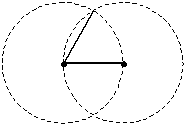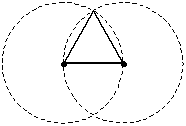
Singole img

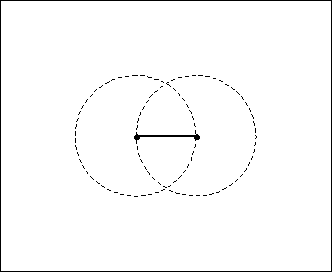
Si vede meglio ?

		dato un lato
		circonferenza con centro su un estremo e raggio uguale al lato
		idem con centro sull'altro estremo
		le 2 circonferenze create si intersecano
		congiungere con segmenti il punto-intersezione e gli estremi del lato.