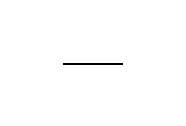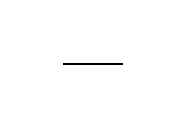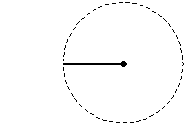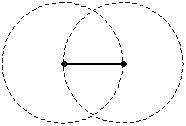
Definizioni 23 | Postulati 5 | Nozioni comuni 5
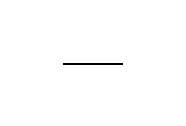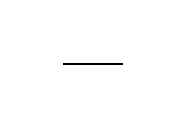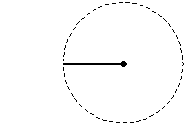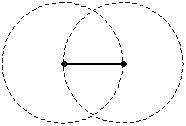
| 1. | Ogni coppia di punti e' connessa da un segmento. |
| 2. | Ogni segmento è prolungabile in linea retta. |
| 3. | Ogni estremo di segmento e' centro di un cerchio avente ii segmento come raggio. |
| 4. | Tutti gli angoli retti sono uguali tra loro. |
| 5. | 2 segmenti tagliati da una trasversale: somma angoli interni dello stesso lato, minore di 2 angoli retti ⇒ i segmenti prolungati da quel lato si incontrano. |
Sebbene i postulati di Euclide affermano esplicitamente solo l'esistenza delle costruzioni, si sottende che le costruzioni sono uniche.
| 1. | disegnare una linea retta tra 2 punti qualsiasi |
| 2. | prolungare un segmento quanto si vuole in linea retta |
| 3. | disegnare un cerchio di dato centro e raggio |
se 2 segmenti che uniscono 2 punti non coincidono, allora 2 linee rette racchiuderebbero uno spazio, il che e' impossibile per definizione4. (un passo in prop4_book1)
"other things being equal, that proof is the better which proceeds from the fewer postulates or hypotheses or propositions."
cit- Hardy 124
Chiedo gogleAI per capire 2
Le superfici in R3 con curvatura di Gauss = 0 in ogni punto, hanno la proprietà fondamentale di poter essere "spianate" su un piano senza subire deformazioni (stiramenti o strappi), poiché sono localmente isometriche al piano euclideo; dette superfici sviluppabili.
Es: cilindro, cilindroide, cono, conoide.
No, non sono sinonimi.
Sebbene siano strettamente correlate, esiste una distinzione gerarchica
fondamentale:
Ecco le differenze principali:
Superfici Rigate: Sono generate dal movimento di una retta (detta
generatrice) lungo una curva. In ogni punto della superficie passa almeno una
retta.
Esempi: iperboloide a una falda; paraboloide iperbolico (la forma delle patatine
Pringles).
Superfici Sviluppabili: Sono superfici rigate speciali in cui il piano tangente alla superficie è costante lungo ogni generatrice. Questa condizione implica che la Curvatura di Gauss sia ovunque nulla. Solo queste possono essere "srotolate" su un piano senza distorsioni.
Il test della curvatura
Per capire se una superficie rigata è anche sviluppabile, si guarda come
cambiano i piani tangenti:
Questa frase significa che gli assiomi classici di Euclide descrivono le proprietà locali e le relazioni geometriche, ma non vincolano la forma globale (la topologia) dello spazio in cui operano.
In parole semplici: puoi avere uno spazio che "obbedisce" a tutte le regole di Euclide in ogni suo punto, ma che visto "da lontano" ha forme molto diverse.
In sintesi, gli assiomi di Euclide ti dicono come si comporta il "tessuto" dello spazio, ma non ti dicono se quel tessuto è un foglio infinito, un tubo o una ciambella.
and therefore we say that a straight line is potentially infinite. To be potentially infinite is in marked contrast to being actually infinite—which would mean that the straight line has no endpoints at all.
"Linea retta" e' intesa corta-finita, lo si induce dal postulato 2 che garantisce di poterla tracciare infinita; anche se prendendolo alla lettera e' "allungare finche' si vuole".
"Linea retta" oggi detto "segmento".
implicitamente: esiste l'angolo-grandezza
Although Euclid's statement of the postulates only explicitly asserts the existence of the constructions, they are also taken to be unique.
| 1 | To draw a straight line from any point to any point. | Ogni coppia di punti e' connessa da un segmento. |
| 2 | To extend a straight line as far as we please in a straight line | Ogni segmento è prolungabile a retta. |
| 3 | To draw a circle whose center is the extremity of any straight line, and whose radius is the straight line itself. | Ogni segmento è raggio di un cerchio. |
| 4 | All right angles are equal to one another. | Tutti gli angoli retti sono uguali tra loro. |
| 5 | If a straight line that meets two straight lines makes the interior angles on the same side less than two right angles, then those two straight lines, if extended, will meet on that same side. | 2 segmenti tagliati da una trasversale, Se gli angoli interni dello stesso lato, sommati sono minori di 2 angoli retti ⇒ prolungati si incontrano da quel lato. |
credits: themathpage/BookI/first
La formulazione italiana e' mia, non mima l'originale, ma ricerca la concisione.