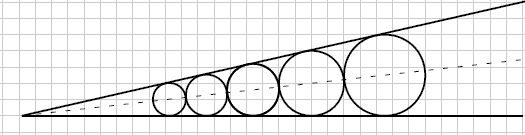

(Per non stereotipare, per non essere bloccati su questo caso che diventa uno stereotipo bloccante, domandiamoci ...)
Teo: |
• retta tangente alla circonferenza
|
|
|
sono tra loro perpendicolari |
Proprieta' base per le dimostrazioni seguenti.

li dove c'e una crc vediamo un tri rtg
c distanza tra vertice dell'angolo e centro della crc e' l'ipotenusa del tri
R raggio della crc, perpendicolare al lato e' un cateto
R/c = sen(β/2) β angolo
Nel caso l'angolo e' fisso e la crc varia, essa varia ma col vincolo
R/c costante.
dim: segmento perpendicolare dal centro al lato e' il raggio della crc
dim: perpendicolare al lato per il punto di tangenza, interseca bisettrice nel centro del crc.
dim: piu' difficile. Prendere ispirazione dal geogebra.
dim: e' la contrazione che porta il punto lontano della crc nel punto vicino della crc, e qyesta contrazione contemporaneamente porta la crc nella sua crc piu' piccola tangente.
(1-x)/(1+x) x=R/c = sen(β/2)
Costruzioni geometriche fondamentali nel librosito.
Studio geometrico di un bicchiere conico.
c1= c0 - (R0+R1)
R0+R1 = R0 + R0(c-R0)/(c+R0)
= R0( 1+ (c-R0)/(c+R0) )
= R0( (c+R0 + c-R0)/(c+R0) )
= R0( 2c0/(c0+R0) )
= R0 2c0/(c0+R0)
c1 = c0 + R0 2c0/(c0+R0)
c1/R1 = R0 2c0/(c0+R0) * (c+R0)/(c-R0)/R0 = 2c0/(c-R)