Una tocca i punti-frazione
| y | ||
| ↔ (x;y) | ||
| x |
A ogni frazione y/x e' associato il punto del piano cartesiano, di coordinate (x;y).
| Frazione |
Coordinate del punto |
|---|---|
| y/x | (x;y) |
Una tocca i punti-frazione
| Frazione y/x | Coordinate (x;y) |
|---|---|
| 1/2 | (2;1) |
| 2/4 | (4;2) |
| 3/6 | (6;3) |
| 4/8 | (8;4) |
| 5/10 | (10;5) |
| Frazione y/x | Coordinate (x;y) |
|---|---|
| 2/3 | (3;2) |
| 4/6 | (6;4) |
| 6/9 | (9;6) |
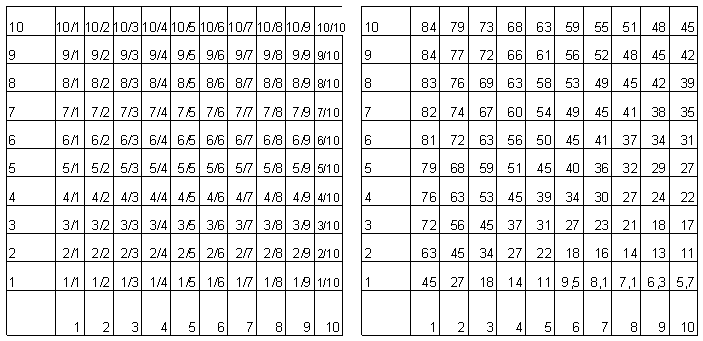
La frazione si puo' interpretare come
| La frazione di ogni punto, scritta nella cella in basso a sinistra del punto; viceversa: il punto associato alla frazione e' vertice in alto a destra della sua cella. | Invece della frazione c'e' l'inclinazione in gradi. Es: alla fraz 1/2 corrisponde inclinaz 27°; 2/3 ↔ 34°; 2/5=4/10 ↔ 22°. |
 |
|
Lo stesso angolo si puo' ottenere con frazioni di diverso numeratore e denominatore, ma tra loro proporzionali, cioe' sono frazioni equivalenti. I triangoli dai lati corrispondenti proporzionali, hanno gli stessi angoli.
Frazione tangente di
un punto del piano cartesiano
a ogni punto del piano cartesiano, di coordinate (x;y), e' associata la frazione y/x.
| Coordinate del punto | Frazione tangente |
|---|---|
| (x;y) | y/x |
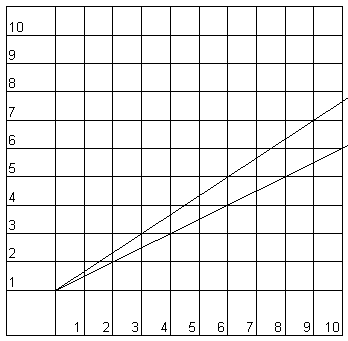
Consideriamo una quadrettatura, vedi fg: 2 rette partono dal punto (0;0). Una tocca i punti
| Coordinate (x;y) | (2;1) | (4;2) | (6;3) | (8;4) | (10;5) |
| Frazione y/x | 1/2 | 2/4 | 3/6 | 4/8 | 5/10 |
l'altra i punti di frazione 2/3 4/6 6/9.
La frazione e' un modo di indicare l'inclinazione; e' un altro modo di indicare lo spostamento orizzontale e verticale.
Inizialmente avevo battezzato la frazione associata al punto "frazione tangente", mettendola in relazione alla tangente trigonometrica, pero' ora, a qualche settimana di distanza, ho dei dubbi a introdurre questa terminologia, che forse posso evitare.