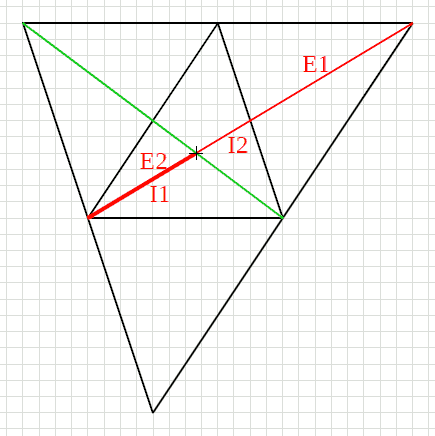
^^Teo: il punto di incrocio di 2 mediane divide la mediana in 2 parti con rapporto 2:1.

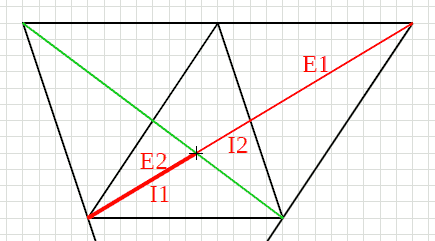1. 2 figure: 2 trilati, 1 esterno, 1 interno dei punti medi,

   corredati con 2 mediane.

2. Le mediane sono divise in 2 parti dal loro punto di incrocio.
   Pensiamo le mediane uscenti dai vertici, e chiamiamo
   1. "parte1" la parte attaccata al vertice
   2. "parte2" la parte dopo l'incrocio

   3. E = E1 + E2  mediana esterna = somma delle sue parti

   4. I = I1 + I2  mediana interna = somma delle sue parti

Struttura, relazioni (tra esterno e interno)

1. similitudine: le 2 figure sono simili
   • la figura esterna e' doppio dell'interna rispetto alla lunghezza, cioe' la costante moltiplicativa e' 2: E=2*I  E1=2*I1  E2=2*I2
2. E2 = I1   parte2 della mediana esterna
                 = parte1 della mediana interna  !!!

Il modo piu' veloce di ragionarla così:

Links

Mediana di un trilato, baricentro.

Approfond: Altri modi di arrivarci, prima di trovare il piu' rapido

In modo generale si scrive una proporzione

l'incognita non e' 1 termine, bensì un rapporto

es:  E1:E2=I1:I2   proporzione tra esterno e interno

E1=2I1  fattore di proporzionalita' 2

E2=I1   relazione geometrica credo equivalente ad essere mediana

(2I1):I1=I1:I2

es:

E:E2=I:I2 = (I1+I2):I2 = I1/I2 +1 = E2/(E2/2) +1 = 2+1 =3

Un altro modo di ragionarla e' con questi valori:

sia

• k  la frazione della parte2 della mediana;
  e' uguale per le mediane corrispondenti interna e esterna poiche' sono simili
• I=1  lunghezza mediana interna

da cui

• 1*k = I2   lunghezza parte2 mediana interna
• 2     = E    lunghezza mediana esterna
• 2*k = E2  lunghezza parte2  mediana esterna

I = I1 + I2 = E2 + I2  = 2k + k

Talk

Dimostrazione "posizione punto di incrocio sulla mediana"