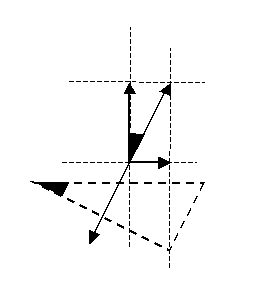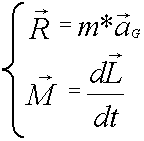Equazioni cardinali della statica; piano inclinato.

Premessa: il soggetto di studio e' il sistema di forze subito da un corpo e il suo equilibrio.

Situazione: Un corpo in equilibrio poggiato su un piano inclinato. Per studiare l'equilibrio del corpo, prima di tutto bisogna individuare le forze subite dal corpo: - la forza peso, distribuita nel volume del corpo - la forza di contatto del piano inclinato, distribuita sulla superficie di contatto.

da non copiare, e non fare durante cc

Disegno delle forze.
Risultanti La risultante delle forze peso e' equilibrata dalla risultante delle forze rimanenti.	Scomposizione, la forza di contatto viene scomposta in 2: forza normale (= perpendicolare) al piano causata dalla non penetrabilita' del piano forza tangenziale causata dall'attrito, da identificarsi con la forza di attrito
	Riconoscere che: - corpo appoggiato su piano inclinato (situaz 1) - e forza inclinata che preme un corpo contro un piano (situaz 2) - hanno lo stesso sistema di forze
da non copiare, e non fare durante il cc

Suggerimenti per il disegno. L'altezza del piano inclinato e' meta' della base: 10base x 5altezza.

pag2

Equazioni cardinali della statica	Definizioni
	R risultante del sistema di forze M momento del sistema di forze

Se il corpo e' fermo,
allora per il corpo e per ogni sua parte valgono le equazioni cardinali.

Le equazioni cardinali sono condizioni necessarie per l'equilibrio;
se il corpo e' rigido,
allora sono anche condizioni sufficienti

Il moto di un corpo dipende: 1: dalle forze agenti sul corpo e 2: dalle condizioni iniziali del moto.

Principio di inerzia, o 1� Principio della dinamica Newton
Parte statica:
- Se la risultante e' diversa da zero, allora il corpo fermo si mette in moto.
- contrapositivo: Se il corpo e' fermo, allora la risultante e' zero.

La risultante nulla non garantisce la stasi.
d: la risultante equivale all'intero sistema di forze?
r: in generale no, come mostrato dalla seguente classificazione.

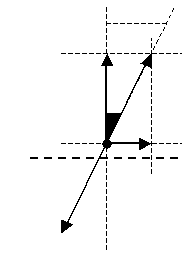
Classificazione dei sistemi costituiti da 2 forze con R=0.
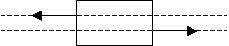
M=0 forze opposte allineate		M≠0 forze opposte non allineate
equilibrio stabile	equilibrio instabile	non equilibrio

Casi in cui la risultante equivale al sistema di forze:
- forze applicate a un PUNTO materiale
- forze ALLINEATE applicate a un CORPO RIGIDO
- FORZA PESO su un CORPO RIGIDO, applicata nel baricentro.

Equazioni cardinali della dinamica	Definizioni
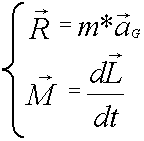	La risultante e' uguale alla massa del corpo per l'accelerazione del centro di massa. Il momento e' uguale alla velocita' di cambiamento del momento angolare.