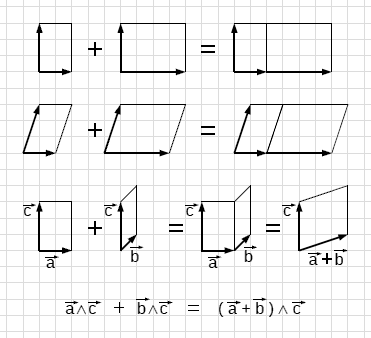
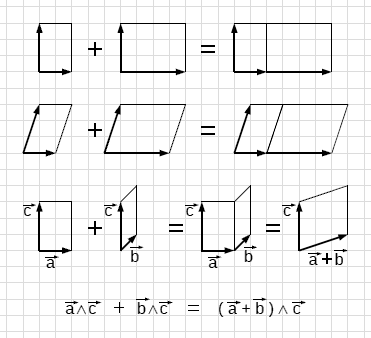
anche le aree si sommano !
anche quando (3ª riga) i lati-vettori da sommare non sono allineati.
Nel caso dei rettangoli, lo aveva mostrato Euclide, Book II, Proposition I.
Per proseguire lo studio, si tratta di vedere come la somma si comporta nei vari casi
Esistono 2 tipi di vt: liberi e applicati; anche per i bvt?
E' uno degli argomenti che mi piacerebbe studiare.
Ambiente: i lati dei rtg sono pensati nell'ordine base altezza.
Nel caso dei rettangoli, usualmente scriviamo
ah + bh = (a+b)h
che si riferisce a: lunghezza dei lati e area dei rettangoli.
| ah | e' il rettangolo di base a e altezza h | |
| ah + bh | e' la somma di 2 rtg di uguale altezza, sovrapponendole estendendo le basi, creando un rtg unione | |
| a+b | e' il segmento somma di 2 seg |
Lo sviluppo di quest'idea e' stato portato a compimento con l'algebra geometrica.
Il rettangolo viene rappresentato da 2 vettori che ne costituiscono i lati
| a∧b | e' il simbolo del bivettore, dove a e b sono i vt che lo definiscono | |
| a∧b | e' orientato, nel senso di 1°vt e 2°vt, che si possono intendere come "base" e "altezza" | |
| ∧ | esplicita l'operazione binaria, detto prodotto esterno o prodotto wedge |
a∧c + b∧c = (a+b)∧c
Invece di usare i segmenti si usano i vettori, che si "sposano" ai nr relativi.
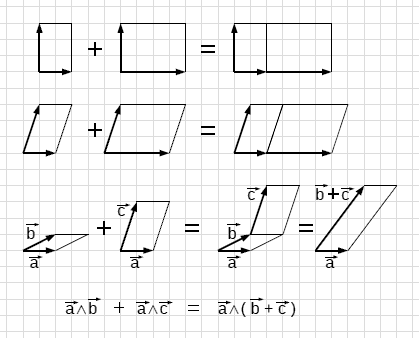
Nel caso dei rettangoli scriviamo
ab + ac = a(b+c)
a∧b + a∧c = a∧(b+c)