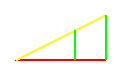

Raffigurare
Le coppie di valori (massa;
prezzo)
si possono raffigurare con un triangolo rettangolo, o un rettangolo, in cui :
massa=base e prezzo=altezza.
(massa; prezzo)
= (base ; altezza).




Che cosa si divide? Una grandezza. In astratto una grandezza, in pratica un sistema.
Che cosa si divide in parti uguali? Una grandezza. In astratto una grandezza, in pratica un sistema.
| Quante parti |
Quanto grandi |
|||||
| 6 | / | 6=2+2+2 | 3 | 2 | ||
| = | 3 | |||||
| 2 | \ | 6=3+3 | 2 | 3 |
| dato: la grandezza delle parti (2) | 2 | 2 | 2 | |||||||
| ++++ | ++++ | ++++ | ++++ | ++++ | ++++ | |||||
| ricavo: il numero di parti | 3 parti | |||||||||
| 6 | / | |||||||||
| = | 3 | |||||||||
| 2 | \ | |||||||||
| dato: il numero di parti (2) | 2 parti | |||||||||
| ++++ | ++++ | ++++ | ++++ | ++++ | ++++ | |||||
| ricavo: la grandezza delle parti | 3 | 3 | ||||||||
| Dato | Ricavo | |||||
| 6 | / | 6=2+2+2 | la grandezza delle parti (2) | ricavo: il numero di parti (3) | ||
| = | 3 | |||||
| 2 | \ | 6=3+3 | dato: il numero di parti (2) | ricavo: la grandezza della parte (3) |
| Pensando solo ai numeri | Interpretazione fisica | ||||
|---|---|---|---|---|---|
| 6 | / | quante volte ci sta? quante_volte ci sta il 2 nel 6? |
misura del 6 rispetto al 2 | ||
| = | 3 | ||||
| 2 | \ | quanto sono grandi le parti? quanto sono grandi le 2 parti del 6? quanto grandi sono 2 parti uguali? grandezza di ognuna delle 2 parti uguali |
grandezza della parte |
| Pensando solo ai numeri | Interpretazione fisica | ||||
|---|---|---|---|---|---|
| 6 m | / | quante_volte il 2 sta in 6 | misura del 6 rispetto al 2 | ||
| = | 3 | ||||
| 2 m | \ | dividere il 6m in 2 parti uguali | grandezza della parte |
| Pensando solo ai numeri | Interpretazione fisica | ||||
|---|---|---|---|---|---|
| 6 euro | / | quante_volte il 2 sta in 6 | misura del 6 rispetto al 2 | ||
| = | 3 | ||||
| 2 m | \ | dividere il 6m in 2 parti uguali | grandezza della parte |
- quante volte il 2m sta in 6m
- dividere il 6m in parti uguali a 2m
operazione: dividere il 6 in 2 parti uguali
risultato:
| Risultato | |||
| / | in parti di fissata grandezza | numero di parti | |
| dividere | |||
| \ | in un fissato numero di parti | grandezza della parte |
Una domanda che risuona nelle orecchie
d: quante volte ci sta?
E' tutto un numero, e ogni numero, lo stesso numero, ha piu' significati a
seconda del suo legame con la realta'.
Anche all'interno dei numeri astratti della matematica:
- dati i numeri
- c'e' il numero di numeri, che ha un significato diverso dai precedenti.
es: 6=3+3; commento: i 3 sono 2. Commento: nel commento precedente "3" e' un
numero base, "2" e' un numero di numeri.
I 2 significati della divisione.
c: 2 sono i significati piu' evidenti, pero' ce ne sono altre.
| 1 | fissato il numero delle parti | Es: dividere la torta in 3 parti. |
| 2 | fissata la grandezza comune delle parti, con un eventuale resto | Es: dividere il tavolo in spanne = quante spanne e' lungo il tavolo. |
c: questa formulazione evidenzia che cmq si tratta sempre di dividere, solo che lo si puo' fare con 2 modalita'.
| 1 | fissato il numero delle parti | di conseguenza la grandezza delle parti | Es: dividere la torta in 3 parti. |
| 2 | fissata la grandezza comune delle parti | di conseguenza il numero di parti, con un eventuale resto | Es: dividere il tavolo in spanne = quante spanne e' lungo il tavolo. |
| Fissato | Di conseguenza | ||
|---|---|---|---|
| 1 | il numero delle parti | la grandezza delle parti | Es: dividere la torta in 3 parti. |
| 2 | la grandezza comune delle parti | il numero di parti, con un eventuale resto | Es: dividere il tavolo in spanne = quante spanne e' lungo il tavolo. |
| Dato: | la grandezza delle parti | 2 | 2u | 2u | 2u | |||
| ++++ | ++++ | ++++ | ++++ | ++++ | ++++ | |||
| Ricavo: | il numero di parti | 3 | 3 parti | |||||
| Dato: | la grandezza delle parti (2) | 2u | 2u | 2u | |||
| ++++ | ++++ | ++++ | ++++ | ++++ | ++++ | ||
| Ricavo: | il numero di parti | 3 parti | |||||
| Dato: | il numero di parti (2) | 2 parti | |||||
| ++++ | ++++ | ++++ | ++++ | ++++ | ++++ | ||
| Ricavo: | la grandezza delle parti | 3u | 3u | ||||
| Dato: la grandezza delle parti (2) | 2u | 2u | 2u | |||
| ++++ | ++++ | ++++ | ++++ | ++++ | ++++ | |
| Ricavo: il numero di parti | 3 parti | |||||
| Dato: il numero di parti (2) | 2 parti | |||||
| ++++ | ++++ | ++++ | ++++ | ++++ | ++++ | |
| Ricavo: la grandezza delle parti | 3u | 3u | ||||
| dato: la grandezza delle parti (2) | 2 | 2 | 2 | |||||||
| ++++ | ++++ | ++++ | ++++ | ++++ | ++++ | |||||
| ricavo: il numero di parti (3) | 3 parti | |||||||||
| 6 | / | |||||||||
| = | 3 | |||||||||
| 2 | \ | |||||||||
| dato: il numero di parti (2) | 2 parti | |||||||||
| ++++ | ++++ | ++++ | ++++ | ++++ | ++++ | |||||
| ricavo: la grandezza della parte (3) | 3 | 3 | ||||||||
es: 3,5 kg di pere a 2,7 euro;
d: 5 kg corrispondono a quanti euro?
d: quanti kg corrispondono a 10 euro?
| kg | euro | |
|---|---|---|
| A | A= 2 kg | A= 3 euro |
| B | B= 4 kg | B = 6 euro |
| kg | euro | euro/kg | |
|---|---|---|---|
| A | A= 2 kg | A= 3 euro | 3euro/2kg = 1,5 euro/kg |
| B | B= 4 kg | B = 6 euro | 6euro/4kg = 1,5 euro/kg |
| B/A | 4kg/2kg = 2 | 6euro/3euro = 2 |
| xAyAxByB | xAxByAyB | ||
| yAxAyBxB | xBxAyByA | ||
:=
| xA:yA=xB:yB | xA:xB=yA:yB | ||
| xB:yB=xA:yA | yA:yB=xA:xB | ||
| yA:xA=yB:xB | xB:xA=yB:yA | ||
| yB:xB=yA:xA | yB:yA=xB:xA | ||
*
| yA*xB | |
| yB= | |
| xA |
| N | x | y |
|---|---|---|
| A | xA | yA |
| B | xB | yB |
| x | y | k=y/x | |
|---|---|---|---|
| A | 2 | 3 | 1,5 |
| B | 4 | 6 | 1,5 |
| m=B/A | 2 | 2 |
 
|
RaffigurareLe coppie di valori (massa;
prezzo)
si possono raffigurare con un triangolo rettangolo, o un rettangolo, in cui : |
    |
E' la forma usata in fisica, poiche' tramite la denominazione mette in evidenza come e' organizzato il sistema sotto studio: in sistemi e variabili.
|
Consideriamo 2 corpi. Di tutte le grandezze misurabili di un corpo, qui si considerano solo: volume e massa - i valori di un corpo "di riferimento": volume_r e massa_r - e i valori dell'altro corpo: volume e massa. |
|
|
In astratto, con le variabili astratte x e y:
|
|
|
Rapporto tra i valori della grandezza omonimaviene interpretato come: |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
|
Rapporto tra i valori di grandezze dello stesso sistemaviene interpretato come: |
Il rapporto tra 2 i numeri di 2 misure esprime la misura di una grandezza rispetto all'altra, in altre parole: quanto una e' piu' grande dell'altra.
Pero' il rapporto si puo' interpretare anche in un altro modo:
quanto del primo termine corrisponde a 1 unita' del secondo termine.