^^Controllare l'inclinazione usando la quadrettatura; inclinazioni ad angolo retto.

 

c: tracciare tutti gli spostamenti proposti di seguito, il cui risultato totale e' il dis .odg|pdf

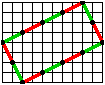
La freccia indica lo spostamento di un punto dal suo inizio alla punta.

Scopo: assegnata una freccia che rispetta la quadrettatura (inizio e fine sui punti di incrocio, detti nodi), imparare a:

Codice colore

colore uguale per le direzioni tra loro perpendicolari, e in nessun altro caso.

Procedimento. Tracciare (+3,+1) con unita' di misura 1q(uadretto)

  1. Tracciare un punto origine nel centro del foglio, circa, ±2q.
  2. Tracciare un riferimento cartesiano con tale origine, di 4 quadranti, cioe' con anche i nr negativi:
  3. Tracciare i punti di partenza-arrivo degli spostamenti.
  4. L'occhio, eventualmente aiutato dal righello, dice che i punti sono allineati. Unire i punti; a mano da un punto al successivo, o con la riga.
  5. L'ultimo tratto-spostamento, terminarlo con una punta, disegnando cosi' una freccia, per rappresentare il verso dello spostamento.
  6. Scrivere il nome dello spostamento vicino alla punta dello spostamento terminale.

 

Ognuno dei tratti, da un punto al seguente, e' uno spostamento vettoriale.

(+3,+1)
e' il nome, simbolo, formula, di ognuno di questi spostamenti vettoriali nel piano.

Tracciare col procedimento precedente, ognuno di questi spostamenti

Simbolo   Significato

(+3;+1)

(+2;+1)

(+1;+1)

(+1;+2)

(+1;+3)

spostarsi 3 a destra, 1 in alto. Gia' fatto.

spostarsi 2 a destra, 1 in alto

spostarsi 1 a destra, 1 in alto

spostarsi 1 a destra, 2 in alto

spostarsi 1 a destra, 3 in alto

Segno del verso degli spostamenti >>>

Notiamo una simmetria, quale ?

Base   Simmetric

(+2;+1)

(+3;+1)

(+1;+1)

(+1;+2)

(+1;+3)

(+1;+1)
  

La simmetria e' scambiare il 1° col 2° elemento.

lg: base, iniziale, partenza, primale, ...

Il simmetrico del simmetrico e' l'oggetto base.

(+1;+1) e' il simmetrico di se' stesso.

Tracciare gli spostamenti perpendicolari (ad uno spostamento)

Gli spostamenti perpendicolari (ad uno spostamento) nel piano sono 2:

Cominciamo con quelli in verso antiorario, nel 2° quadrante.

 

D: Quali sono le coordinate dello spostamento:

  1. ruotato di 1 angolo retto antioriario ?
  2. ruotato del ruotato = opposto
  3. ruotato del ruotato del ruotato = ruotato orario
Base   Rot +90° Opposti Rot -90°
(+1;+1)

(+2;+1)

(+3;+1)

(+1;+2)

(+1;+3)

 (-1:+1)

(-1:+2)

(-1:+3)

(-2:+1)

(-3:+1)

 (-1;-1)

(-2;-1)

(-3;-1)

(-1;-2)

(-1;-3)

 (+1:-1)

(+1:-2)

(+1:-3)

(+2:-1)

(+3:-1)

 

D: Qual e' la regola ? >>>

Base   Rot +90° Opposti Rot -90°
(x;y) (-y;x) (-x;-y) (y;-x)

Links

  1. Le rotazioni di 1/4 di giro si rappresentano facilmente per mezzo delle coordinate cartesiane.
  2. esOf: Spostamento obliquo scomposto in uno spostamento orizzontale e uno verticale.

Approfond

Arrivo mag2016

per disegnare correttamente Braccio efficace in cc Rotazione e Torcente.

Links

Spostamento multiplo di uno spostamento.

 

lg: Variazioni

  1. assegnata una freccia sulla quadrettatura, e che la rispetta (inizio e fine sui punti di incrocio), imparare a ...

Guida ins

Tb orientativa per aiutare la valutazione

1 -0,1 disposizione malfatta. Es: (x;y) → (-y;x)
2 -0,1 mancano le punti
3 -0,5 uguale multiplo 5, non rispettato
4    
5 -0,1 scrivere coordinate spostamento male o sbieche
6 -0,3 mancata o errata scrittura (x;y) → (-y;x)
7 -0,5 manca una direzione nel disegno
8 -0,5 punte non comprese nella lunghezza del segmento
9    
10    
11    
12    

 

Titolo

  1. Scheda: "Spostamenti di inclinazione controllata costante, ed inclinazioni ad angolo retto".
  2. Scheda: "Controllare l'inclinazione usando la quadrettatura; inclinazioni ad angolo retto".

Scopo:

imparare a tracciare un segmento perpendicolare ad uno assegnato.
2) Prolungare il segmento.