^^Braccialetto elastico. Singola variabile.

? Come la densita' lineare di forza varia al

Vedere se e' possibile calcolare la dipendenza dalle singole variabili, piu' facilmente della formula totale comprendente la dipendenza da tutte le variabili.

Fare cio' permette di sviluppare l'intuizione fisica.

Teo: la "stretta" e' dir prop alla tensione: f= kT (a parita' di circolo-raggio)

dim: moltiplicando per m la tensione e la f, si hanno risultanti moltiplicate per m, che se erano in equilibrio prima lo sono anche ora.

2 archi di circonferenza, uno di raggio il doppio dell'altro.

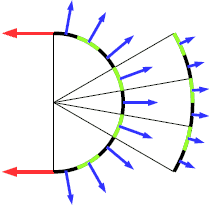
frecce blu: densita' di forza subita ai lati.

Le frecce sono vettori proporzionati all'intensita'.

Sull'arco di raggio doppio la densita' di forza e' la meta'.

Precisiamo il campo di densita' di forza: in ogni punto perpendicolare alla fune, e intensita' uniforme.

Da cui:

La forza risultante su archi corrispondenti di raggio diverso, e' uguale poiche' estensione dell'arco e densita' sono inversamente proporzionali. Questo sarebbe vero nel caso scalare, ma qui sono vettori, ed e' da provare, e per ora diciamo intuitivamente che e' cosi'. Allora in entrambi gli archi abbiamo le stesse forze, quindi la stessa risultante, che deve equilibrare la stessa forza ai capi. Viceversa se le tensioni sono le stesse, allora devono essere le densita' inversamente proporzionali ai raggi.

L'operazione che fa passare dal campo di densita' alla sua risultante.

ref: Densita' di forza. Forza risultante di un sistema di densita' di forze.

Teo: la "stretta" e' inversamente proporzionale alla lunghezza della circonferenza, quindi al raggio f=k/R (a parita' di tensione)

dim: perche' si mantenga l'equilibrio, dato che la forza di tensione non cambia, allora la risultante della forze laterali non deve cambiare; quindi quando il circolo cambia estensione, la stessa forza laterale deve distribuirsi sulla stessa zona ridimensionata.

Approfondimento

2 archi di circonferenza, uno di raggio il doppio dell'altro.

Interpretiamo il disegno. Supponiamo le frecce siano vettori proporzionati alle forze. La forza laterale non cambia densita' sulle 2 circonferenze. La forza risultante sulla zona corrispondente, e' doppia poiche' l'estensione e' doppia. Questa conclusione non e' esattamente vera poiche' le 2 forze non sono parallele. E' approssimazione per piccoli angoli, che diventa esatta nell'infinitesimo.

Supponiamo che le frecce siano vettori proporzionati alla densita' di forza

precisiamo il campo di densita' di forza dicendo che deve essere perpendicolare alla fune. In tal caso occorre dare un senso all'operazione che fa passare dal campo di densita' alla sua risultante. ref: Densita' di forza. Forza risultante di un sistema di densita' di forze.