^^Equilibrare un'asta appesa scentrata, con 1 peso. Rel 2017.

 
Questa e' la relazione, se invece si vuole indagare-approfondire.

Le foto qui a lato sono illustrative, non da copiare. Idem per la piccola animaz dell'asta oscillante.

Descrizione del fenomeno

Un corpo appeso ad un perno-fulcro che non passa per il baricentro del corpo , oscilla; fino a fermarsi nella sua posizione di equilibrio stabile.
Interpretazione: il peso del corpo, distribuito su tutto il volume, crea un torcente che fa ruotare il corpo.

Azione sperimentale: equilibrare il torcente fatto dal peso distribuito del corpo, appendendo un pesetto al corpo.

Teoria

Il peso, distribuito sul volume di un corpo rigido (moltissime piccole forze), equivale

Scopo:

Calcolare il torcente equilibrante, e confrontarlo col torcente causato dal baricentro scentrato.

Materiali

  1. Leva del laboratorio.
  2. 4 pesi da 10g; 3 da 50g
  3. elastichino
  4. dinamometro 100gf

Svolgimento: equilibrare coi pesetti

Misurare il peso dell'asta col din100gf. Misurato con la bilancia, mediamente sulla popolazione di leve e' 85gf.

  1. Infilare il perno nel foro che realizza il voluto braccio del baricentro bG.
    Per fare con ordine: spostare di 1 foro ogni volta, partendo dal baricentro, quindi  bG = -2 -4 -6 ... -14 cm.
  2. Per ogni braccio e' stato previsto che pesetto equilibrante usare.
    Usare il pesetto equilibrante, e modificarne braccio fino a realizzare l'equilibrio.
  3. Registrare il valore del braccio equilibrante.
  4. Ripetere cambiando il fulcro, passando al foro seguente.

 

Disegno, Commento alla figura .odg|pdf

D: Perche' usare "G" per indicare il bari-centro ?
R: G ≡ gravita'. Baricentro ≡ centro di gravita' (del corpo).

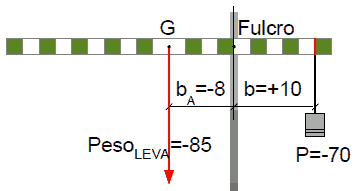
Nel caso in figura:

le misure dei bracci b sono in cm, non in quadretti

MG = bG·FG = -8cm·(-85gf) = +680cm·gf

M = b·F = +10cm·(-70gf) = -700cm·gf

D%(|M|;|MG |)= (700-680)/680*100 = +2,9%

 

Progettiamo l'esp

I calcoli seguenti servono per progettare le misure da fare, proposte piu' avanti.

Decidiamo:

Calcoliamo-scegliamo i peso equilibrante. Come fare? Si puo' per tentativi, ma per velocita' vorremmo gia' scegliere quello giusto.

Idea che puo' aiutare: quant'e' la forza equilibrante applicata al foro estremo?

Tb braccio-forza-torcente per prevedere la forza equilibrante

forza equilibrante applicata al foro estremo, il suo braccio e' dal fulcro al foro estremo.

Scopo tb: calc la forza che equilibra il torcente del peso del corpo (dato il suo braccio).

  Misure Calcoli
N bG FG MG b F F
  cm gf cm*gf cm gf gf
1 -2 -85 170 18 -9,4 -10
2 -4 -85 340 16 -21,3 -30
3 -6 -85 510 14 -36,4 -40
4 -8 -85 680 12 -56,7 -60
5 -10 -85 850 10 -85,0 -90
6 -12 -85 1020 8 -127,5 -130
7 -14 -85 1190 6 -198,3 -200
8 -16 -85 1360 4 -340,0 N.D.
9 -18 -85 1530 2 -765,0 N.D.

Legenda

Ultima colonna: forza arrotondata ai 10g superiori (di intensita'), che sono i valori di forza disponibili in laboratorio coi pesetti.

MG bG FG   momento torcente, braccio, forza, della forza peso totale FG della leva, applicata nel baricentro.
M b F   momento torcente, braccio, forza, del pesetto equilibrante
N.D.   Non Disponibile

Formule

MG=bGFG    MG+M=0   F=M/b

Calc .ods

 

Tb braccio-forza-torcente equilibrante.

Chi non ha i propri dati, usare quelli riportati piu' avanti.
    mis previst mis   previst  
bG F b M=-MG M=bF D% b=MG/F D%
cm gf cm cm*gf cm adim cm adim
-2 -10   -170     17,0  
-4 -30   -340     11,3  
-6 -40   -510     12,8  
-8 -60   -680     11,3  
-10 -90   -850     9,4  
-12 -130   -1020     7,8  
-14 -200   -1190     6,0  

 

D%   differenza percentuale tra valore previsto e valore misurato; previsto preso come riferimento.
D% =  |mis|-|previst|

|previst|

 *100    i nr presi in valore assoluto

D% Torcente equilibrante misurato VS previsto

D% Braccio equilibrante misurato VS previsto

Scala di valutazione dell'insegnante:

D% < 3% ottimo, < 5% buono, < 8% sufficiente, >8% insufficiente.

Conclusione

I risultati sperimentali concordano con le previsioni teoriche con una differenza percentuale massima del ....  .

 

Dati di esempio, a chi servono

Tb braccio-forza-torcente equilibrante. 1Atec_23-3-2018

usando la minima forza equilibrante realizzabile coi pesetti

    mis previst mis   previst  
bG F b M=-MG M=bF D% b=MG/F D%
cm gf cm cm*gf cm adim cm adim
-2 -10 16,9 -170 -169 -0,6 17,0 -0,6
-4 -30 11,6 -340 -348 +2,4 11,3 +2,4
-6 -40 12,8 -510 -512 +0,4 12,8 +0,4
-8 -60 11,7 -680 -702 +3,2 11,3 +3,2
-10 -90 9,6 -850 -864 -1,6 9,4 -1,6
-12 -130 8,0 -1020 -1040 +2,0 7,8 +2,0
-14 -200 6,1 -1190 -1220 +2,5 6,0 +2,5

D: perche' per  bG=-6, si ha  D%(bmis;bpre)=+0,4%  invece di 0, dato che in entrambi i casi il valore riportato del braccio b e' 12,8 ?

 

Approfond

Versione stampa.htm|.pdf

Svolgimento: equilibrare col dinamometro

rendersi conto che:

  1. se si applica la forza nel baricentro, allora la forza equilibrante vale il peso della leva
  2. se si applica la forza a distanza dal baricentro uguale alla distanza che il baricentro ha dal fulcro, allora la forza equilibrante vale la meta' del peso della leva.

Spiegarsi il perche'.

 

Versione "tante piccole tb"

Da compilare Compilate
   

Tb ms braccio equilibrante

usando la minima forza equilibrante realizzabile coi pesetti

bG F b
cm gf cm
-2 -10  
-4 -30  
-6 -40  
-8 -60  
-10 -90  
-12 -130  
-14 -200  

 

Tb ms braccio equilibrante

usando la minima forza equilibrante realizzabile coi pesetti

bG F b
cm gf cm
-2 -10 16,9
-4 -30 11,6
-6 -40 12,8
-8 -60 11,7
-10 -90 9,6
-12 -130 8,0
-14 -200 6,1

 

Torcente equilibrante previsto VS misurato

  previst mis  
bG M=-MG M=bF D%
cm cm*gf cm adim
-2 -170    
-4 -340    
-6 -510    
-8 -680    
-10 -850    
-12 -1020    
-14 -1190    

 

Torcente equilibrante previsto VS misurato

  previst mis  
bG M=-MG M=bF D%
cm cm*gf cm adim
-2 -170 -169 -0,6
-4 -340 -348 +2,4
-6 -510 -512 +0,4
-8 -680 -702 +3,2
-10 -850 -864 -1,6
-12 -1020 -1040 +2,0
-14 -1190 -1220 +2,5

 

Braccio equilibrante previsto VS misurato

  previst mis  
bG b=M/F b D%
cm cm cm adim
-2 17,0    
-4 11,3    
-6 12,8    
-8 11,3    
-10 9,4    
-12 7,8    
-14 6,0    

 

Braccio equilibrante previsto VS misurato

  previst mis  
bG b=M/F b D%
cm cm cm adim
-2 17,0 16,9 -0,6
-4 11,3 11,6 +2,4
-6 12,8 12,8 +0,4
-8 11,3 11,7 +3,2
-10 9,4 9,6 -1,6
-12 7,8 8,0 +2,0
-14 6,0 6,1 +2,5

 

Dirlo

Il peso distribuito sul volume di un corpo rigido (moltissime piccole forze), equivale

Il peso distribuito sul volume di un corpo rigido, equivale

  1. all'azione di una forza uguale al peso totale, applicata nel baricentro
  2. alla forza peso totale, applicata nel baricentro
  3. al peso totale, applicato nel baricentro

La definizione di D% puo' essere leggermente diversa

D% = ((M-MG)/min(M;MG))*100    presi i nr in valore assoluto

Oss:

il minimo peso equilibrante sara' quello, tra i possibili pesi equilibranti, col massimo braccio.

 

Guida ins

 

Legenda

cmt: con grandezze separate, cioe' 1 alla volta, ma credo sia meglio raggruppare in unita' funzionale

bG   braccio della forza del peso totale FG della leva, applicata nel baricentro.
b   braccio del pesetto equilibrante, applicato sul braccio corto.
FG   forza peso totale della leva
F   Forza del pesetto equilibrante
MG   momento torcente del peso della leva
M   momento torcente del pesetto
MT   momento torcente totale
D%   differenza percentuale tra i 2 momenti torcenti