^^Circonferenza-arco approssimat con una parabola. Parabola osculatrice.

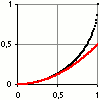
es Elevazione del pendolo approssimata con una parabola

	Circonferenza		Parabola osculatrice
R=1	y=1-√(1-x2)		y= 1 2 x2
R≠1	y=R-√(R2-x2)		y=x²/(2R)
	y R =1-√(1- ( x R ) 2 )		y R = 1 2 ( x R ) 2

Calc .xls|.ods

Riporto alla forma canonica del cerchio goniometrico

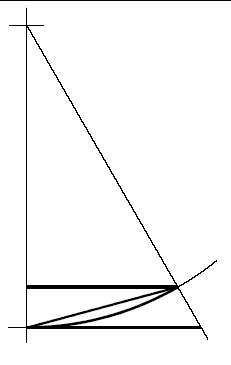
		l'elevazione della circonferenza e' il senoverso, freccia della circonferenza goniometrica

La circonferenza col punto basso coincidente con l'origine del piano cartesiano, e' approssimata dalla parabola  y=(1/R)*(1/2)*x².

La circonferenza unitaria e' approssimata dalla parabola y=(1/2)*x² .

Idea: La somiglianza tra parabola e circonferenza si puo' usare nei 2 versi.

Posso approssimare:

• la circonferenza con la parabola, ad es per avere una dipendenza espressa da una funzione matematica piu' semplice
• la parabola con la circonferenza, ad es per calcolare il raggio di curvatura

Elevazione in funzione dell'ampiezza. Calcolo esatto col teo di Pitagora. ref: Pendolo. Elevazione in funzione dell'ampiezza.

Confronto tra circonferenza e parabola

L'errore % non cambia passando a figure proporzionali, numeri proporzionali

Links

1. Curvatura di una linea; raggio di curvatura; circonferenza osculatrice, cerchio osculatore, piano osculatore, parabola osculatrice.
2. Seno, tangente, angolo, arco e corda uguali in prima approssimazione, per piccoli angoli.
3. Circonferenza approssimata da una parabola.xls
4. ix Parabola.

5. esOf: Approssimare.

    

Guida ins

Titolo

1. Circonferenza-arco approssimat con una parabola. Parabola osculatrice.
   c: originale
2. Circonferenza approssimata con una parabola.

VS

y/R=1-√(1-(x/R)²)

Vecchia versione che voleva tenere tutto assieme

Circonferenza unitaria Parabola osculatrice y=1-√(1-x2)   .xls|.ods y= 1 2 x2