
 .odg|pdf
.odg|pdf
| t | s | t | s | |
|---|---|---|---|---|
| 1 | 1 | 2 | 4 | |
| 1,1 | 2,2 | |||
| 1,2 | 2,4 | |||
| 1,3 | 2,6 | |||
| 1,4 | 2,8 | |||
| 1,5 | 3,0 | |||
| 1,6 | 3,2 | |||
| 1,7 | 3,4 | |||
| 1,8 | 3,6 | |||
| 1,9 | 3,8 | |||
| 2 | 4 | 4 | 16 |

| t | s [frazT] |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 4 | 16 |
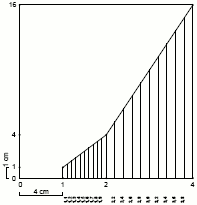
Conosciamo questi punti del grafico, 3, generati dalla regola "½ t ¼ s".
|
La scelta di queste di sequenze di numeri e' perche' una e' il doppio dell'altra, come valori, es: 1,1*2 = 2,2 1,2*2 = 2,4 1,3*2 = 2,6 ...
Ricordiamoci che questo e' un esercizio per indirizzarci alla meta finale
| t | s | ∆s |
|---|---|---|
| 1 | 1 | 3 |
| 2 | 4 | |
| 1,1 |
Desidererei fare un tracciato che finisse sui mm interi. Studio le condizioni. 1) A ogni ∆t=+0,1, ∆s dovrebbe crescere di +1mm o 2 o 3, insomma un nr intero di mm. E quindi nei 10 passi ∆t=+0,1, ∆s dovrebbe crescere di 10 mm o 20 o 30 o un multiplo di 10. Questo incremento e' quello da t=1 a t=2, e quindi e' 3 volte quello da t=0 a t=1, cioe' reciprocamente ∆s(0;1) = (1/3) ∆s(1;2), e quindi perche' ∆s(0;1) sia intero, deve essere ∆s(1;2) multiplo di 3. Unendo le 2 condizioni, ∆s(1;2) deve essere multiplo di 10 e di 3; l'unica scelta pratica per il foglio A4 e' UMs = 10mm.
UMt = 20 mm, o 30 o 40.
| t | ∆t | s | ∆s | t | ∆t | s | ∆s | |
|---|---|---|---|---|---|---|---|---|
| 1 | +1 | 1 | +3 | 2 | +2 | 4 | +12 | |
| 2 | 4 | 4 | 16 | |||||
| /10 | /10 | /10 | /10 | |||||
| +0,1 | +0,3 | +0,2 | +1,2 | |||||
| 1 | +0,1 | 1 | +0,3 | 2 | +0,2 | 4 | +1,2 | |
| 1,1 | idem | 1,3 | idem | 2,2 | idem | 5,2 | idem | |
| 1,2 | 1,6 | 2,4 | 6,4 | |||||
| 1,3 | 1,9 | 2,6 | 7,6 | |||||
| 1,4 | 2,2 | 2,8 | 8,8 | |||||
| 1,5 | 2,5 | 3,0 | 10 | |||||
| 1,6 | 2,8 | 3,2 | 11,2 | |||||
| 1,7 | 3,1 | 3,4 | 12,4 | |||||
| 1,8 | 3,4 | 3,6 | 13,6 | |||||
| 1,9 | 3,7 | 3,8 | 14,8 | |||||
| 2 | 4 | 4 | 16 |
| t | ∆t | s | ∆s | t | ∆t | s | ∆s | |
|---|---|---|---|---|---|---|---|---|
| 1 | +0,1 | 1 | +0,3 | 2 | +0,1 | 4 | +0,6 | |
| idem | 2,1 | idem | 4,4 | idem | ||||
| 1,1 | 1,3 | +0,3 | 2,2 | 5,2 | ||||
| 2,3 | 5,8 | |||||||
| 1,2 | 1,6 | +0,3 | 2,4 | 6,4 | ||||
| 2,5 | 7 | |||||||
| 1,3 | 1,9 | +0,3 | 2,6 | 7,6 | ||||
| 2,7 | 8,2 | |||||||
| 1,4 | 2,2 | +0,3 | 2,8 | 8,8 | ||||
| 2,9 | 9,6 | |||||||
| 1,5 | 2,5 | +0,3 | 3,0 | 10 | ||||
| 3,1 | 10,6 | |||||||
| 1,6 | 2,8 | +0,3 | 3,2 | 11,2 | ||||
| 3,3 | 11,8 | |||||||
| 1,7 | 3,1 | +0,3 | 3,4 | 12,4 | ||||
| 3,5 | 13 | |||||||
| 1,8 | 3,4 | +0,3 | 3,6 | 13,6 | ||||
| 3,7 | 14,2 | |||||||
| 1,9 | 3,7 | +0,3 | 3,8 | 14,8 | ||||
| 3,9 | 15,6 | |||||||
| 2 | 4 | 4 | 16 |
Rem: Il rapporto incrementale di segmenti paralleli e' uguale.
In particolare: Il rapporto incrementale di segmenti dello stesso segmento e'
uguale.